对结构承受的极值风压进行概率分析, 给出具有确定保证率的设计风荷载, 是结构风工程领域的热点问题之一。根据经典极值理论, 只要有足够多的相互独立的随机样本, 即可根据样本极值序列建立极值概率分布模型, 获得具有确定保证率的极值^[1,2]。但是由于需要大量的风洞试验或实测数据样本作为支持, 因而这种方法在实际工程中难以应用。在实际工程中, 人们往往希望通过少量样本实现对极值风压的准确估计。在这方面, 国内外学者已进行了较多研究, 提出了若干方法。这些方法可大致分为两类:第一类是基于样本母体分布假定来推断样本极值, 其代表性方法是峰值因子法^[3], 该方法假定脉动风压母体分布为高斯分布, 进而结合零值穿越理论推导出风压极值期望值与脉动风压标准差之间的关系。近年来对大跨屋盖的风荷载特性研究表明, 在屋盖的边、角、脊等区域的风压具有明显的非高斯特征, 此时采用峰值因子法将会得到偏于不安全的估计结果。为解决此问题, Kareem等人^[4,5]将非高斯过程表示为考虑高阶统计量的高斯过程的Hermite多项式, 从而将峰值因子法扩展到非高斯过程中。Sadek和Simiu^[6]利用等效概率原则^[7]将非高斯过程转化为高斯过程, 提出一种针对非高斯过程的极值计算方法。然而, 样本极值分布仅与母体分布的尾部形状有关, 而与其中央的形状无关, 导致上述方法获得的结果对母体分布尾部表现出很强的灵敏度, 可能出现较大误差。另一类方法是基于样本独立峰值而由少量样本来直接推断样本极值, 其代表性方法是Cook^[8]提出的“独立风暴”法, 该方法的基本思路是, 提取风速 (或风压) 连续超过阈值的数据段作为一个“独立风暴”, 取每个“独立风暴”的峰值作为极值分析的样本;将极值Ⅰ型分布作为样本极值的概率模型, 采用最小二乘法进行参数估计^[4]。最小二乘法进行参数估计时会引入新的系统误差, 对此Harris^[9]采用加权最小二乘法进行极值分布模型未知参数的估计, 获得样本极值的最优无偏估计。可以看出, 第二类估计方法无须先估计样本母体分布, 即可直接得到样本极值分布, 继而得到具有确定保证率的估计极值。

　　 本文借鉴应用于极值风速预测的“独立风暴”法及其改进方法, 发展了一种更具效率的极值概率分析方法———基于“风压脉冲”的极值风压估计方法, 以解决大跨屋盖结构极值风压的概率估计问题。然后, 基于平面屋盖和球面屋盖风洞试验多次独立采样获得的大量风荷载样本, 建立起较为精确的极值风压概率模型, 将其估计结果作为评价基于少量样本的极值估计方法估计结果准确性的标准, 对本文方法与改进“独立风暴”法 (Modified Independent Storms Method, MIS) 进行比较, 验证本文改进方法的有效性。最后, 将本文方法应用于某实际工程大跨屋盖结构极值风压的估计中, 给出具有了确定保证率的设计风荷载, 使得屋盖围护结构设计的安全性得到了极大的提高和保证。

　　 识别出样本的独立峰值以充分利用样本时程的信息, 是小容量样本极值估计方法需要解决的首要问题。“独立风暴”法^[8]提取样本里的独立峰值的基本步骤是:设定某一阈值c_t;将连续低于阈值c_t的时间序列记为峰谷, 相邻峰谷之间的时间序列即为“独立风暴”, 这样从风压时程样本识别出若干的“独立风暴”;将各“独立风暴”的最大值作为最终的极值分析对象。对于某段风压时程, 图1给出了按照上述操作得到的峰值结果。

　　 利用样本里拾取的独立峰值建立起样本极值的概率模型, 是小容量样本极值估计方法需要解决的重要问题。设从R段样本时程共识别出N个独立峰值{c₁, …, c_N}, 假设各样本中独立峰值出现频率一致, 即任意样本中独立峰值数目没有显著波动, 则各样本的独立峰值数r=N/R。假设识别出的独立峰值c为独立同分布的随机变量, 且单个独立峰值的概率分布函数为G^︿ (c) , 则单个样本极值的概率分布为:

　　 Cook^[8]的“独立风暴”法和Harris^[9]改进方法均以极值Ⅰ型为单个样本极值的概率分布G (c) 的渐进分布, 即存在:

　　 式中α, Π均为待定分布参数。

　　 对式 (2) 进行简单变换, 可得到关于分布参数的线性函数:

　　 将式 (3) 代入式 (2) 可得:

　　 对提取出的独立峰值按照降序进行排列即可获得独立峰值的经验分布函数, 得到第i个峰值c_i对应的估计量:

　　 式中, i=1时对应提取峰值的极大值c₁, i=N对应提取峰值的极小值c_N。将 (P_i) ^r作为对[G_i^︿ (c) ]^r的估计, 通过式 (4) 由最小二乘法即可获得分布参数的估计值。然而这一估计过程可能引入新的系统误差, 因此有必要在进行参数估计前计算各独立峰值对应-ln[-ln G (c) ]的无偏估计。根据文献[9], 令, 则i阶值对应ξ的无偏估计函数表达式为:

　　 式中:f_i (z) 为对应i阶值的z的概率密度函数;y_i^—为对应i阶值的-ln[-lnz]的无偏估计。

　　 将称作绘图位置, 则这一估计过程没有引入系统误差。同样地, 可以获得i阶值对应ξ的标准差σ_i。此时待定分布参数α和Π可以通过加权最小二乘法确定, 计算公式如下:

　　 式中w_i为加权系数,

　　 将上述参数估计值代入极值I分布模型中, 即可获得不同累积概率p的极值估计值:

　　 基于“独立风暴”思想的峰值选取方法并不能从理论上保证提取的峰值具有统计独立性。对此, 吴迪等^[10]通过风压时程自相关分析获得使相邻峰值相关性足够小的时间间距, 然后对“独立风暴”法的峰值进行再次选择。赵明伟等^[11]给出了更为严格的独立峰值提取方法, 峰值除了满足上述条件外, 相邻峰值之间存在着均值穿越。然而风压样本时程的峰值提取结果表明, 后两种改进方法的峰值提取结果几乎相同, 主要原因是时间间距取值较大, 使得后者的相邻峰值之间均值穿越的条件自动满足。上述改进方法获得相邻峰值的时间间距取值过大, 虽然能够保证识别出的峰值满足独立性要求, 都是使得获得独立峰值个数偏少。一般地, 屋盖表面测得的风压信号在时域内间歇性地出现很大的负向脉冲, 这种现象被称作为“风压脉冲”现象。“风压脉冲”是瞬间、随机出现的, 因此从“风压脉冲”现象识别出的峰值满足独立性要求。同时, 风压脉冲是屋盖表面风荷载的一个重要表现形式^[12], 因此从风压脉冲识别独立峰值更具物理意义。对此, 本文将采用基于“风压脉冲”峰值的提取方法, 具体步骤为:1) 确定某一阈值, 凡是超过此值的观测值均列入统计序列, 再对得到的序列进行分析;2) 从序列中找出用以描述“风压脉冲”事件的四个点:事件发生点、其前后与均值的交叉点以及事件的峰值点 (图2所示的3, 1, 2, 4号点) ;3) 提取“风压脉冲事件”的峰值点, 作为后续极值分布概率模型的分析对象。

　　 对于本文的峰值提取方法, 阈值的取值较小时, 得到的统计序列相关性较强, 不能保证峰值的独立性;而阈值的取值较大时, 得到的峰值信息过少, 不能进行后续的极值分析。确定阈值的基本原则是在满足跨越阈值次数服从泊松分布的前提下保留尽可能多的独立峰值。下面介绍一种阈值的选择方法:

　　 设定某一阈值u, 样本母体分布为F (x) , 则样本里超于阈值u的概率p=1-F (u) 。由二项式概率的泊松逼近定理可知, 如果n→∞, p→0使得np=λ保持为正的常数, 则下式对k=0, 1, 2, …一致成立:

　　 式 (10) 右侧是参数为λ的泊松分布。式 (10) 说明, 当满足定理的条件时跨越阈值次数服从泊松分布。在实际计算中, 当n≥10, p≤0.1时, 可以应用上式计算超越阈值的概率。因此, 设定的阈值应满足u≥F^-1 (0.90) 。

　　 可以看出, 本文的峰值提取方法不用通过相邻峰值的时间间距保证相邻峰值的独立性。对于同一段风压时程, 本文方法的峰值提取结果如图2所示。

　　 典型屋盖形式的极值风压概率分布特征研究表明, 存在着极值风压不服从极值Ⅰ型分布的情况^[10]。此时采用MIS法的极值概率模型进行极值估计, 存在着独立峰值{c₁, …, c_N}与相应的绘图位置呈现出非线性关系的情况 (图3) 。这情况得到的极值估计结果将与精确值有很大的偏差, 说明极值Ⅰ型分布不能作为样本极值的概率分布模型。与极值Ⅰ型相比, 广义极值分布包含了3种极值分布形式, 具有更广的适用性, 弥补了单独采用某一种极值分布函数的不足。然而小容量样本里提取的峰值数目往往有限, 往往难以满足广义极值分布拟合时所需的极值样本数目要求, 此时仍然采用广义极值分布模型进行极值估计, 将不能获得精确的参数估计结果。

　　 为了表示绘图位置与独立峰值之间的非线性关系, 本文引入中间变量Z, 计算公式如下:

　　 式中:C为独立峰值变量;C_s为尺度参数, 即C_s=1/α, 而α由MIS法的参数估计获得, 则Z为无量纲数;k为使Z与ξ^—的相关系数取最大值时的参数值。

　　 此时得到Z和绘图位置ξ^—有较好的线性关系, 即有:

　　 类似地采用加权最小二乘法进行未知参数的估计, 最终得到加权最小二乘法的离差平方和:

　　 容易得到未知参数的具体表达式:

　　 此时, 具有保证率p的极值估计值x_p可由下式获得:

　　 可以看出k值等于1时, 改进的极值概率模型会退化成MIS法的极值概率模型。

　　 风洞试验在哈尔滨工业大学的风洞与浪槽联合实验室中进行, 试验对象为平面屋盖和球面屋盖刚性模型, 平面屋盖的几何缩尺比为1∶50, 球面屋盖的几何缩尺比为1∶100, 风速缩尺比为1∶2。平面屋盖模型跨度为800mm, 长跨比为1∶1, 下部支座高度为200mm。球面屋盖模型跨度为600mm, 矢跨比为1∶5, 下部支座高度为120mm。试验地面粗糙度类别为B类, 试验风速为15m/s, 采样频率为625Hz, 采样时长为12s。根据相似比, 平面屋盖和球面屋盖换算到原型结构上的时间分辨率分别为0.04, 0.08s, 采样时长为5, 10min。在平面屋盖模型表面共布置289个测点, 测点布置如图4 (a) 所示;在球面屋盖模型表面共设置217个测点, 测点布置如图4 (b) 所示。通过编制软件实现自动重复采样功能, 在保证所有条件均不变的情况下, 试验中对球面屋盖和平面屋盖分别进行1 411次、1 001次独立采样。所有采样信号利用管路频响函数进行了修正, 以消除信号畸变的影响。

　　 各测压点上的风压值采用无量纲压力系数表示:

　　 式中:C_pi (t) 为模型上第i号测压孔的风压系数;P_i (t) 为该位置处测得的表面风压值;P₀与P_∞分别为参考点处的平均总压与平均静压, 参考点位置为屋盖顶部高度。

　　 各样本风压系数时程的最大值和最小值为该样本的最不利正压系数和最不利负压系数。风压符号的约定为:风压力为正, 风吸力为负。

　　 为了验证本文方法的有效性, 本文利用屋盖风洞试验1 000多次独立采样获得的样本极值信息, 基于经典极值理论, 建立屋盖极值风压的概率分布标准模型———广义极值分布模型, 进而获得各保证率的极值估计值, 以评价本文改进方法极值估计结果的准确性。其中, 广义极值分布为:

　　 式中:μ为位置参数;σ为尺度参数;k为形状参数, k=0时为极值Ⅰ型分布, k>0时为极值Ⅱ型分布, k<0时为极值Ⅲ型分布。

　　 广义极值分布的3个特征参数须满足1+k (x-μ) /σ>0, 其中形状参数最为重要, 决定了极值分布类型。对于最不利风压系数, 图5给出了平面屋盖和球面屋盖中线测点的形状参数, 从图5可以看出:1) 对于平面屋盖, 2~6号测点的形状参数值小于0, 符合极值Ⅲ分布;7号测点的形状参数值接近于0, 可认为其符合极值Ⅰ型分布;其他测点的形状参数值大于0, 符合极值Ⅱ型分布;2) 对于球面屋盖, 17号测点的形状参数值大于0, 符合极值Ⅱ型分布;而其他测点的形状参数值小于0, 符合极值Ⅲ分布。

　　 屋盖中线测点上具有57%和95%保证率的最不利风压系数估计值如图6所示, 下文将以其作为评价基于少量样本的极值风压估计方法准确性的标准。

　　 考虑到实际工程中屋盖模型风洞试验常用的独立采样次数, 本文考察了样本容量为10时的极值估计结果。基于平面屋盖和球面屋盖1 000多次独立采样的风压系数时程样本, 随机生成500组样本容量为10的组合样本, 并采用上述方法估计的极值风压。为了方便比较, 首先定义了估计相对值Z和估计值偏离系数δ两个指标, 计算公式如下:

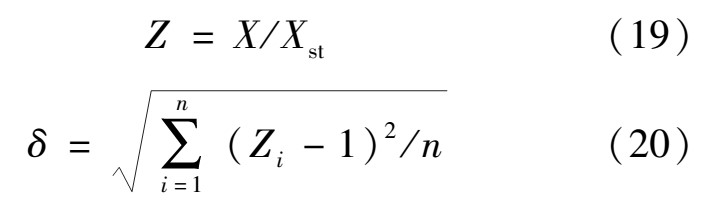
　　 式中:X, X_st分别为极值估计值、标准值;Z_i为第i组样本的估计相对值;n为样本分组总数。

　　 估计值偏离系数可以综合衡量极值估计结果的准确性和稳定性。

　　 图7和图8分别给出样本容量为10时, 平面屋盖和球面屋盖中线上各测点57%保证率 (极值Ⅰ型分布的极值期望值) 和95%保证率的极值估计结果。从图中可以看出:1) 低保证率的极值估计结果优于高保证率的极值估计结果, 可见, 获得准确的高保证率的极值估计值需要更大的样本容量;2) 由图7 (a) , (b) 和图8 (a) , (b) 可知, 本文方法计算结果离散性较大, 估计平均值大于MIS法且接近于准确值;3) 由图7 (c) , (d) 和图8 (c) , (d) 可知, 本文方法的极值估计效果优于MIS法, 表现在:对于本文方法, 平面屋盖中线各测点上57%保证率的估计值偏离系数在0.08以内, 95%保证率的估计值偏离系数在0.14以内, 球面屋盖中线测点上57%保证率的估计值偏离系数在0.07以内, 95%保证率的估计值偏离系数在0.11以内;相对地, MIS法在平面屋盖1号、9~17号和球面屋盖的17号测点上的估计效果差。

　　 综上所述, 与MIS法相比, 本文方法通过较小容量样本即可建立起相对精确的目标概率模型, 获得较为稳定、准确的极值估计结果。

　　 鄂尔多斯市冰雪运动中心由冰球馆及室内滑雪场两部分组成, 建筑效果及模型图如图9所示。试验在哈尔滨工业大学风洞与浪槽联合实验室中进行, 风洞试验模型为刚性模型, 采用有机玻璃和ABS板制成, 风洞试验风向角见图10。考虑风洞阻塞率的要求 (不超过5%) , 模型几何缩尺比选为1∶200。试验基本风速为10m/s, 模拟B类地貌风场, 实际风速为54.7m/s, 风速比为1∶5.47。测压信号采样频率为625Hz, 采样时间为20s, 根据相似比换算到原型结构上的时间分辨率为0.06s, 总时长为730s。试验时, 模型固定在试验段底壁转盘上, 由0°开始逆时针旋转至345°, 每隔15°测量一次, 进行了24个风向的测量。其中, 对0°风向角进行了150次独立采样, 其他风向角只有3次独立采样。

　　 0°风向角的试验工况共进行150次独立采样, 利用经典极值理论可以建立起较为精确的极值概率模型, 将其估计值作为标准值。样本容量较少, 广义极值分布拟合时难以获得精确的极值估计结果;而屋盖的不同位置风荷载极值可能服从不同极值分布, 采用极值Ⅰ型分布拟合可能带来较大的误差。采用蒙特卡洛模拟法对比不同极值分布的估计结果, 确定选用广义极值分布为极值分布模型。图11分别给出了冰球馆屋面具有57%, 95%保证率的极值风压系数估计值分布云图。

　　 应用本文提出的基于“风压脉冲”的极值风压估计方法对0°风向角下的风压时程数据进行分析, 获得具有57%, 95%保证率的极值风压系数估计值, 其分布云图如图12所示。

　　 由图11, 12可以看出, 采用本文方法得到的极值风压系数估计值在数值上接近于标准估计值, 并且二者分布规律一致。说明本文方法通过较少容量的样本建立的极值概率模型能够实现相对精确的、具有确定保证率的极值估计。

　　 针对实际工程的大跨屋盖结构极值风压概率估计问题, 本文提出了针对少量样本的极值风压估计方法———基于“风压脉冲”的极值风压估计方法。主要结论有:

　　 (1) 提出了基于“风压脉冲”的独立峰值拾取方法, 并改进了MIS法的极值概率模型, 实现了对样本极值的最优估计。

　　 (2) 结合平面屋盖和球面屋盖的多次采样风洞试验, 将本文方法应用于屋盖表面极值风压的估计, 并与MIS法进行对比, 结果表明, 本文方法通过较小容量样本即可建立起相对精确的目标概率模型, 获得较为准确的极值估计结果。

　　 (3) 通过将本文方法应用于实际工程屋盖结构的极值风压估计中, 验证了本文方法的有效性和可行性。