水平荷载作用下高层建筑受力与非受力层间位移计算
0 前言
我国《建筑抗震设计规范》 (GBJ 11—89)
在几十年的设计实践中, 由于高层建筑层间位移角对结构设计的影响很大, 有时甚至起着决定性的影响, 导致结构工程师对这一限值科学合理性的讨论和争议从未间断。究其原因主要是规范定义的层间位移为相邻上、下层的层位移之差, 层间位移角为层位移差除以相应层高, 但却未能清楚说明此层间位移角的内涵和组成, 更未给出明确的量化计算公式。本文拟从源头剖析层间位移的组成及内涵, 在此基础上提出相应的计算方法并给出工程案例说明其应用, 为今后逐步解决工程界对高层建筑层间位移角限值这一重大设计控制问题的争议和歧见提供理论依据和说明, 可供规范修订和设计参考。
1 层间位移组成剖析
1994年, 文献
需要指出的是, 层间位移
构件顶端位移用下式表示:
由此得到i层构件j的层间位移
式中:Δsi, j为受力层间位移 (有害位移) ;Δri, j为非受力层间位移 (刚性位移或无害位移) , Δsi, j, Δri, j可分别表示为:
式中Δim, j, Δiv, j分别为单位弯矩及剪力作用下构件;相应的顶端位移, 当构件为等截面杆时:
式中EIi, j为i层任一竖向构件j的截面抗弯刚度。
式 (2) 清楚表明, 层间位移由受力层间位移和非受力层间位移两部分组成, 并不是单一的受力位移, 随着构件底端θi-1, j的增大, 非受力层间位移的占比将相应增大。当结构底端为嵌固端时, 转角为零, 即θ0=0, 此时首层非受力层间位移Δr1, j为零, 层间位移
由式 (1) 可知, i>1时各楼层层间位移必大于该层的受力位移, 如下式:
式中n为楼层数。
随着楼层位置增高, i增大, 在水平荷载作用下任意层竖向构件底端均发生同向转角, 每层均相应出现非受力层间位移Δri, j, 其值逐步增大, 当θi-1, j在结构中上部达到较大值时, 结构层间位移
大量案例分析说明, 除顶部竖向构件和结构刚度较差的情况外, 一般最大受力层间位移Δsi发生在首层, 即:
最大层间位移
2 受力与非受力层间位移的计算
对于一个n层的高层建筑, 受力构件一般由柱和剪力墙组合构成, 设i层柱为mc个, 墙为ms片, 则在水平荷载作用下任一柱非受力位移Δrc, i, j可由下式计算:
当柱为等截面矩形杆时, 其受力位移Δsc, i, j为:
式中:Mc, i, j, Vs, i, j为i层柱j顶部的弯矩与剪力;Ic, i, j为i层柱j的截面惯性矩;θc, i-1, j为i层柱j底端的转角。以上各值均由结构整体分析结果给出。
当剪力墙为矩形截面杆时, 由于墙计算模型的不同, 计算方法略有差异, 当将剪力墙视为与柱相同的杆件时, 其非受力层间位移Δrs, i, j的计算与式 (8) 相同, 即:
其受力层间位移Δss, i, j为:
式中:Is, i, j, As, i, j为i层j段剪力墙的截面惯性矩与截面面积;μ为截面剪力分布不均匀系数;Ms, i, j, Vs, i, j为i层j段剪力墙顶部的弯矩与剪力;θs, i-1, j为i层j段剪力墙底端转角。
当将剪力墙作为壳元按有限元方法分析时, 平截面假定严格意义上已不存在, 可按以下方法近似计算, 将剪力墙段在竖向划分为k个单元, 取各单元底端转角平均值为剪力墙底端转角θks, i-1, j, 即:
式中θs, i-1, j, p为剪力墙划分k个单元后对应的单元剪力墙底端转角。
此时剪力墙非受力层间位移Δrks, i, j可近似由下式计算:
墙顶的受力层间位移, 可由有限元分析求得顶部各单元节点内力, 并合成剪力墙截面弯矩和剪力后, 按式 (13) 近似计算求得。以上所有计算中均认为柱与墙顶端的轴力作用于截面形心, 轴力作用下不产生受力位移。
由此可见, 高层建筑的受力与非受力层间位移, 并非是以一个楼层为单元给出的同一结果, 而是通过这一楼层各竖向构件不同的受力与非受力层间位移结果来表达。
3 一些情况分析
3.1 假定楼板平面内为无限刚
(1) 对称结构
当结构对称, 假设各层楼板平面内无限刚时, 结构各楼层i的层位移在水平荷载作用下只有唯一值Δi, 而由于楼层i的层间竖向构件底端产生的转角θi-1, j不同, 相应由θi-1, j引起构件顶端的非受力位移Δri, j也不同, 因此, 其顶端的受力位移也必然不同, 两者之和为该层的层间位移
(2) 不对称结构
在水平荷载作用下, 不对称结构任意楼层i产生扭转角φi, 如图2所示, 这时竖向构件Ci, j还产生由扭转引起的附加位移φiai, j, 该处层间位移
式中:
3.2 斜柱
如图3所示, 斜柱顶端和底端的水平位移分别为Δi, j和Δi-1, j, 层间位移为
当构件为等截面杆时, i层的受力层间位移为:
式中:Ni, j为斜柱j顶端的轴力值;α为斜柱的倾角;Ai, j为斜柱j截面面积。
当斜柱变直柱时, α=0, 式 (17) 即退化为式 (11) 。剪力墙一般垂直于楼层, 斜墙相应计算公式本文不讨论。
3.3 嵌固端位于地下室底板
当嵌固端取在地下室底板时, 由于地下室四周土的约束及地下室外墙的巨大抗侧刚度等因素, 地下室各楼层的水平位移可近似取为零, 但地下室顶板 (即结构首层底端) 处各柱、墙的转角不为零 (θ0, j≠0) , 即首层层间位移
3.4 假设整个楼层为平截面, 楼板平面内为无限刚
水平荷载作用下, 实际结构在各楼层竖向构件的底端均产生不同的转角。当假设结构整个楼层在水平荷载作用下符合平面假定时, 各楼层产生同一转角, 层间各竖向构件底端的转角θi-1, j必然相同, 此时所有层间竖向构件顶端的非受力层间位移Δri相同;当楼板平面内为无限刚时, 任意楼层i也出现同一层间位移, 由于各竖向构件顶端层间位移
由此可见, 只有在各楼层整个维持平截面且假定楼板为面内无限刚的特定情况下, 同一楼层才有相同的受力位移和层间位移。
4 工程案例
4.1 案例一
4.1.1 结构概况
海口市某酒店采用框架-核心筒结构, 结构平面及墙柱编号见图4, 地面以上24层, 结构高度为98.5m (属于B级高度) , 结构高宽比为2.88。结构构件主要尺寸及混凝土强度等级见表1。50年一遇基本风压w0为0.75kN/m2, 地面粗糙度类别为B类, 风荷载体型系数为1.4。抗震设防烈度为8度, 设计基本地震加速度为0.3g, 设计地震分组为第二组, 阻尼比为0.05。小震设计时, 风荷载作用下的变形较小, 为地震作用控制。经验算, 风荷载和地震作用下墙柱构件的变形规律相近, 本文仅给出墙柱构件在风荷载作用下的变形情况。
结构构件主要尺寸及混凝土强度等级 表1
|
构件名称 |
构件尺寸/mm | 混凝土强度等级 |
|
梁 |
300×800, 500×1 200, 300×800, 400×900, 400×700 |
C40~C35 |
|
板 |
首层厚200;屋面层厚120~150; 其他层厚100~150 |
C40~C35 |
|
柱 |
从下往上:1 200×1 200~700×700 | C60~C35 |
|
剪力墙 |
从下往上:核心筒外墙厚650~250, 内墙厚300~200 |
C60~C35 |
4.1.2 结构周期
采用PKPM, MIDAS Gen软件求得结构前6阶自振周期及结构总质量如表2所示, 计算结果表明, 两个软件计算结果很接近, 以下采用MIDAS Gen软件进行进一步计算。
结构自振周期及结构总质量 表2
|
结构主要指标 |
计算程序 |
||
|
PKPM |
MIDAS Gen | ||
|
主要自振周期/s |
T1 |
2.33 | 2.43 |
|
T2 |
2.18 | 2.21 | |
|
T3 |
1.66 | 1.68 | |
|
T4 |
0.75 | 0.71 | |
|
T5 |
0.61 | 0.62 | |
|
T6 |
0.59 | 0.62 | |
|
结构总质量/ (×104t) |
6.14 | 6.05 | |
4.1.3 墙柱底端转角
计算结果表明任一楼层墙柱底端转角均不相同, 说明整个楼层转角不符合平截面假定。X向风荷载作用下, 10层墙柱最小转角发生在柱8、柱9, 其值为0.44×10-3rad, 其余墙柱底端转角均大于此值, 其余墙柱底端转角与最小转角 (柱8、柱9转角) 的比值见图5。由图可见, 墙底端转角明显大于柱底端转角, 最大差值率接近20%。Y向风荷载作用下, 10层墙柱底端转角的最小值发生在柱4, 其值为0.42×10-3rad, 其余墙柱底端转角均大于此值, 其余墙柱底端转角与最小转角 (柱4转角) 的比值见图6。由图可见, 墙底端转角明显大于柱底端转角, 最大差值率接近20%。选取柱3、墙1和墙4, 其底端转角沿高度的变化见图7, 说明墙柱底端转角在底部楼层最小, 在中上部楼层最大, 而顶部楼层略微减小。
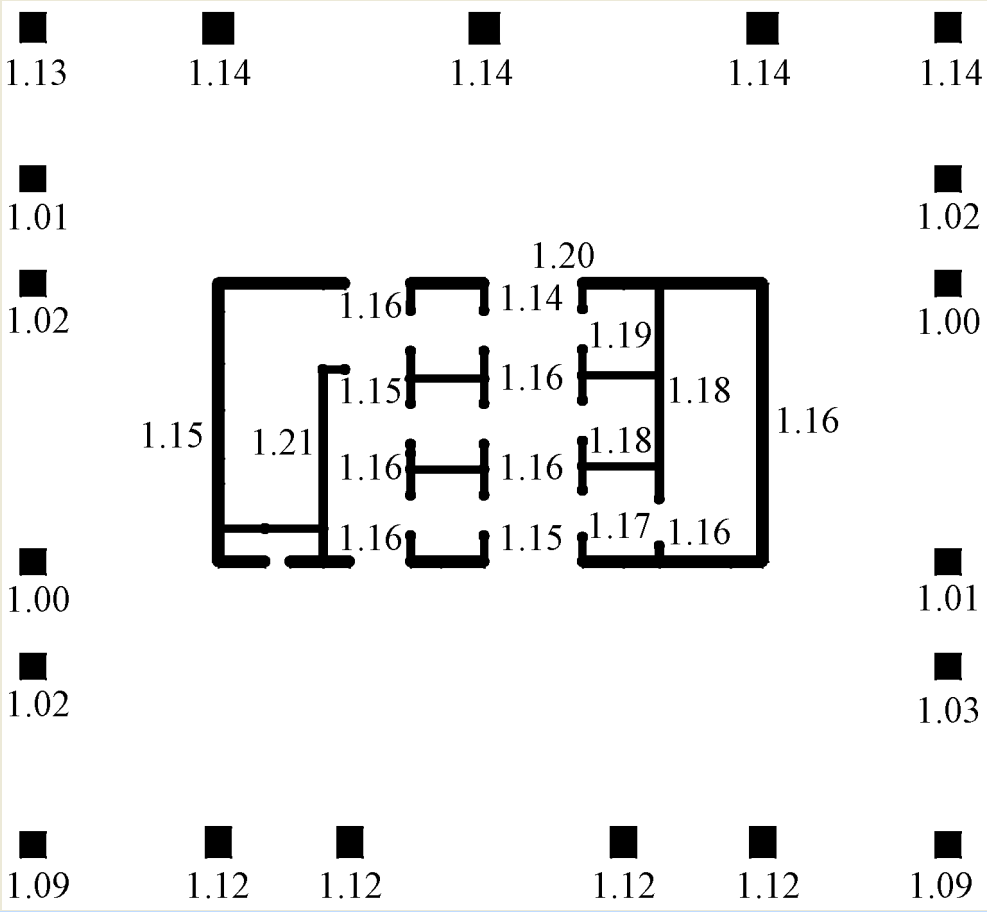
图6 Y向风荷载作用下10层墙柱转角比值分布
4.1.4 墙柱层间位移角
风荷载作用下, 选取柱3、墙1和墙4, 采用前文所述的计算方法, 得出其受力层间位移角、非受力层间位移角及层间位移角沿高度的变化曲线, 如图8, 9所示。由图可见, 结构受力层间位移角数值一般均很小, 且沿高度略有减小 (顶部柱因结构原因除外) , 当底部为嵌固端时, 结构首层墙柱受力层间位移角与层间位移角相等, 且数值最大为1.16×10-4;结构首层墙柱的非受力层间位移角为零, 随着结构高度增加, 非受力层间位移角迅速增大, 与相应楼层层间位移角数值逐渐接近, 甚至相等。
经分析, 最大层间位移角发生在结构中上部, 柱3非受力层间位移角与层间位移角接近, X, Y向非受力层间位移角与相应层间位移角之比分别为89%, 82%, 非受力层间位移角与相应受力层间位移角之比分别为8.5, 4.5;核心筒墙肢的受力层间位移角与相应层间位移角之比较柱的更小, X, Y向的非受力层间位移角与相应层间位移角之比分别为93%, 98%, 非受力层间位移角与相应受力层间位移角之比分别为12.9, 39.3。
4.2 案例二
4.2.1 工程概况
本项目塔楼采用框架-核心筒结构, 有4个带伸臂的加强层, 分布在沿高度约50, 100, 150m及200m处。结构平面及墙柱编号见图10。室外地面到塔楼主要屋面共65层, 结构高度为253.8m (属于超B级高度) , 高宽比为11.03。结构构件主要尺寸及混凝土强度等级见表3。深圳地区50年一遇的基本风压w0为0.75kN/m2, 地面粗糙度类别为B类。风荷载体型系数为1.4。抗震设防烈度为7度, 设计基本地震加速度为0.10g, 设计地震分组为第一组, 阻尼比为0.05。小震计算分析时, 结构为风荷载控制, 在风荷载作用下的变形较大。特别是Y向迎风面较大, 且刚度较弱, 结构Y向在风荷载作用下最大层间位移角较大, 本文给出墙柱构件在Y向风荷载作用下的变形情况。
4.2.2 结构周期
分别采用YJK, MIDAS Gen软件求得结构前6阶自振周期及结构总质量如表4所示, 结果表明两个软件计算结果很接近, 采用MIDAS Gen软件进行进一步的计算。
4.2.3 墙柱底端转角
计算结果表明任一楼层墙柱底端转角均不相同, 说明整个楼层转角不符合平截面假定。Y向风荷载作用时, 33层墙柱底端转角的最小值发生在柱3, 其值为2.197×10-3rad, 其余墙柱底端转角均大于此值, 其余墙柱底端转角与最小转角 (柱3转角) 的比值见图11。由图可见, 墙底端转角明显大于柱底端转角, 最大差值约4%。选取柱1、墙1和墙2, 其底端转角沿高度的变化见图12, 说明墙柱底端转角在底部楼层最小, 在中上部楼层最大, 顶部楼层略微减小。
4.2.4 墙柱层间位移角
选取柱1、柱2、墙1、墙5, 采用前文所述的计算方法, 得出其受力层间位移角、非受力层间位移角及层间位移角沿高度的变化曲线, 如图13, 14所示。由图可见, 结构受力层间位移角数值一般均很小, 且沿高度略有减小 (加强层位置除外) , 当底部为嵌固端时, 结构首层墙柱受力层间位移角与层间位移角相等, 且数值最大为2.42×10-4;结构首层墙柱的非受力层间位移角为零, 在加强层位置, 受力层间位移角为负值。随着结构高度增加, 非受力层间位移角迅速增大, 与相应楼层层间位移角数值接近。
结构构件主要尺寸及混凝土强度等级 表3
|
构件名称 |
构件尺寸/mm | 混凝土强度等级 |
|
梁 |
700×800, 1 000×800, 500×700, 500×800 | C35 |
|
板 |
首层厚200;屋面层厚120~150; 其他层厚120~180 |
C35 |
|
柱 |
从下往上:2 000×2 000~800×800 | C60~C45 |
|
剪力墙 |
从下往上:核心筒外墙厚1 000~600, 内墙厚600~500 |
C60~C45 |
注:柱为型钢混凝土柱, 钢材型号为G345。
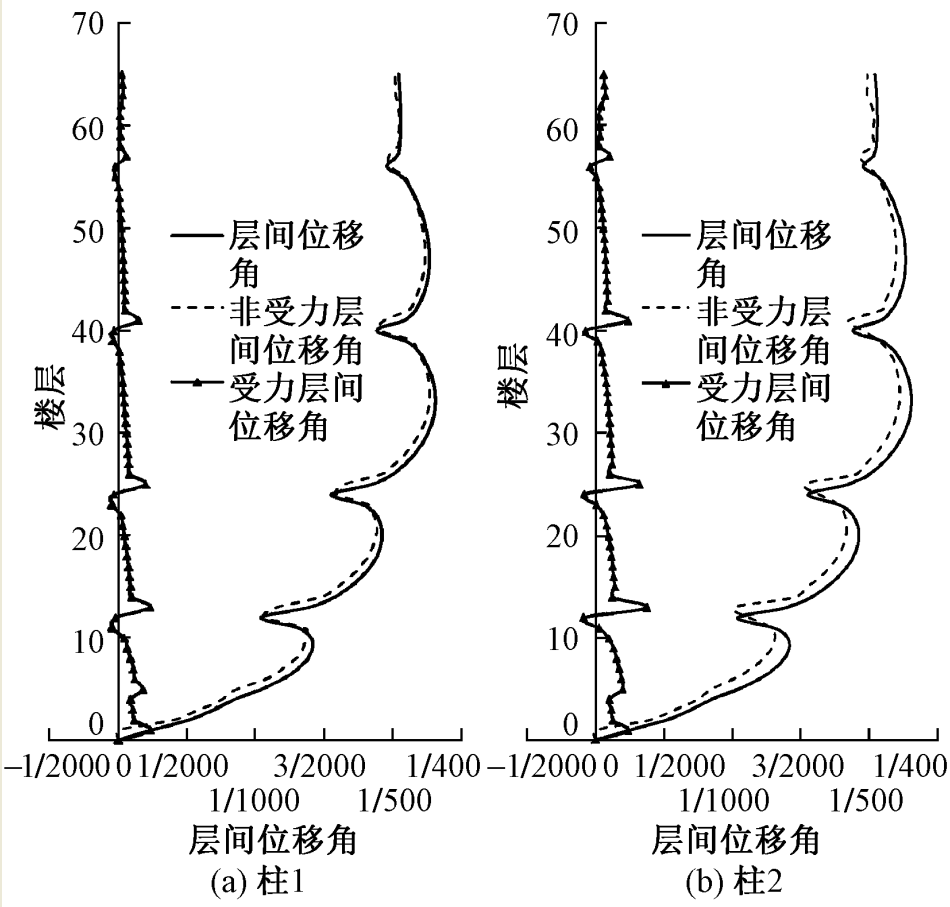
图13 Y向风荷载作用下柱1、柱2层间位移角
结构自振周期及结构总质量 表4
|
结构主要指标 |
计算程序 |
||
|
YJK |
MIDAS Gen | ||
|
主要自振周期/s |
T1 |
6.27 | 6.21 |
|
T2 |
4.19 | 4.31 | |
|
T3 |
3.44 | 3.66 | |
|
T4 |
1.57 | 1.61 | |
|
T5 |
1.17 | 1.24 | |
|
T6 |
1.03 | 1.07 | |
|
结构总质量/ (×104t) |
15.54 | 15.61 | |
经分析, 最大层间位移角发生在结构中上部, 墙柱非受力层间位移角与层间位移角接近, 除加强层及其相邻楼层外, 柱Y向的非受力层间位移角与相应层间位移角之比为98%, 非受力层间位移与相应受力层间位移之比达53;核心筒墙肢受力层间位移角与相应层间位移角之比较柱的更小, Y向非受力层间位移角与相应层间位移角之比约为98%, 非受力层间位移与相应受力层间位移之比达62。
5 结论
(1) 楼板按弹性分析时, 各墙柱层间位移差均不相同, 结构层间位移实质上不能用单一结果表达。当假定楼板为面内无限刚时, 楼层各墙柱的层间位移差是相同的, 可以给出该楼层层间位移角的唯一值。当结构有扭转时, 需考虑扭转角的附加影响。
(2) 层间位移由受力层间位移和非受力层间位移两部分组成, 两者之和等于该楼层相应墙柱的层间位移。当楼板为面内无限刚时, 各墙柱的层间位移相等, 但各墙柱的非受力层间位移与受力层间位移是不同的。
(3) 楼层各墙柱的非受力层间位移为其底端的转角θi, j-1与层高的乘积, 计算方便, 在结构整体分析中软件可给出各墙柱底端转角的数值, 可方便简捷求出所有墙柱的非受力层间位移;楼层各墙柱的受力层间位移可由整体分析求出的顶端内力按悬臂杆得到。当楼层为面内无限刚时, 楼层的层间位移由相邻上下层的位移差给出。
(4) 通过两个工程案例计算可知, 高层建筑楼层的受力层间位移角很小。在本文的两个案例中, 首层受力层间位移角最大, 非受力层间位移角在首层为0 (嵌固端在±0标高时) , 随着高度增加其值迅速增大, 在中高部位达最大值。由此可见, 规范规定的高层建筑最大层间位移角限值其主要目的实际上不是控制结构受力的安全性。
(5) 弹性层间位移角的大小对非结构构件及设备运行是有影响的, 当非结构构件及设备运行对层间位移角有明确和较严要求时, 设计应满足相应的限值要求。
[2] 钢筋混凝土高层建筑结构设计与施工规定:JZ 102—79 [S].北京:中国建筑工业出版社, 1979.
[3] 魏琏.地震作用下建筑结构变形计算方法[J].建筑结构学报, 1994, 25 (2) :2-10.
[4] 魏琏.高层建筑结构位移控制研讨[J].建筑结构, 2000, 30 (6) :27-30.
[5] 魏琏, 王森, 韦承基.水平地震作用下不对称不规则结构抗扭设计方法研究[J].建筑结构, 2005, 35 (8) :19-27.











