随着城市经济的发展, 城市建筑开始呈现出向高层化发展的趋势。框架-核心筒结构是高层、超高层建筑中常用的结构体系之一。通常框架-核心筒结构建筑会将核心筒布置在楼层平面的中心位置, 从而兼顾建筑功能要求及结构抗震的平面布置规则性要求。但是目前出现的一些有特殊建筑功能要求的高层建筑及建筑方案要求采用不规则的平面形状, 提出了将核心筒偏离中心位置甚至偏置于结构一侧的特殊要求。此类核心筒偏置结构在竖向荷载与水平地震作用下, 其受力性能与核心筒居中布置的框架-核心筒结构相比存在较大的不同。

　　 目前关于偏置结构受力性能的理论研究不够系统, 且其中有相当大一部分研究对象还只是针对单层结构^[1], 对高层及超高层框架-偏置核心筒结构设计的参考意义不大。而在建或已建成的工程中在应对此类核心筒偏置结构时, 通常是根据工程师的经验或概念分析而采用相应的补强措施, 并未能将此类结构的设计经验加以总结进而形成相应的设计理论。

　　 本文通过建立一系列的数值计算模型, 对核心筒偏置的框架-核心筒结构在竖向重力荷载及水平地震作用下的受力性能进行了较为全面的分析, 可为该类结构的设计提供参考。

　　 在目前已有的理论研究中, 通常根据偏心的类型不同, 将偏心结构划分为刚度偏心体系 (SES) 和质量偏心体系 (MES) 两类^[2]。刚度偏心体系的结构抗侧力构件刚度分布不对称但质量分布对称, 而质量偏心体系的结构楼层平面质量分布不对称但刚度分布对称。这样的类型划分虽有利于理论上的推导, 但由于在实际的高层建筑结构中, 核心筒的偏置将同时产生质量的不对称分布和刚度的不对称分布, 因而几乎不可能出现单纯的刚度偏心体系或质量偏心体系, 所以这样的理论分类并不适合直接用于实际结构设计及分析。

　　 结合工程经验及国内外实际工程案例, 根据核心筒偏置的成因, 将核心筒偏置高层建筑结构划分为三类:第一类偏置结构是由于建筑平面形状不规则, 引起核心筒的偏置, 例如上海北外滩白玉兰广场酒店 (图1 (a) ) ^[3];第二类偏置结构虽然建筑平面形状规则, 但是由于建筑功能或方案设计而人为要求核心筒偏置, 例如上海小东门C2塔楼 (图 1 (b) ) ;第三类偏置结构是由于核心筒沿高度不对称收进从而导致的部分楼层核心筒偏置, 例如上海世茂总部大楼 (图1 (c) ) 。本文针对其中应用最为广泛的第二类偏置结构进行研究。

　　 本文搜集了若干国内目前在建或已经建成的较为有代表性的核心筒偏置结构案例^{[3,4,5,6,7,8,9,10,11]}, 以及笔者公司设计的部分项目案例, 列于表1中。此类建筑从结构设计角度而言大都属于超限建筑。超限指标主要集中在结构高度超限及扭转位移比超限两个方面。

　　 假定高层结构为均匀悬臂杆, 整体变形以弯曲变形为主, 质量和刚度沿高度均匀分布, 总高为H, 高宽比为λ。结构平面为正方形, 边长为a, 则λ=H/a, 核心筒偏置距离为d (图2) 。因核心筒偏置而导致的刚度偏心矩为e, 则偏心率为γ=e/a。

　　 定义核心筒相对于平面边长的偏移率η₁为:

　　 $\eta {}_1=\frac{d}{a}(1)$

　　 核心筒的截面面积比η₂为:

　　 $\eta {}_2=\frac{A{}_{\text{w}}}{A{}_{\text{w}}+A{}_{\text{c}}}(2)$

　　 式中:A_w为核心筒截面面积;A_c为外框柱的截面面积之和。

　　 结构的扭转效应最终宏观表现为扭转位移比的大小, 因此扭转位移比是判断实际扭转效应大小的重要指标。下面推导结构顶部楼层的扭转位移比计算公式。若水平地震作用为F, 地震作用因偏心引起的扭矩为T, 则:

　　 ${\rm T}=Fe=F\gamma a(3)$

　　 结构在地震作用下的变形可分解为平动变形和绕刚心的扭转变形, 则平动变形u为:

　　 $u=\frac{F{\rm H}{}^3}{3E{\rm I}}(4)$

　　 式中:E为结构的弹性模量;I为所有竖向构件按平截面假定计算得到的惯性矩。

　　 结构扭转角φ为:

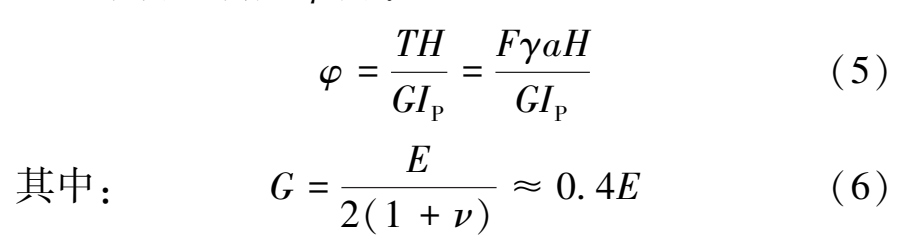
　　 式中:G为结构的剪切模量;I_p为结构的极惯性矩;ν为结构的泊松比, 对于混凝土结构近似取0.25。

　　 由扭转引起的结构平面远端平动位移u₁为:

　　 对于正方形平面, 可近似假定I/I_P≈1/2, 从而式 (12) 可表示为:

　　 $\zeta =\frac{1+3.75(0.5\gamma +\gamma {}^2)/\left(\frac{{\rm H}}{a}\right){}^2}{1+3.75\gamma {}^2/\left(\frac{{\rm H}}{a}\right){}^2}(13)$

　　 假定外框柱的截面面积之和为A_c, 核心筒的截面面积为A_w, 为方便起见近似假定平面刚心与形心重合, 则:

　　 $\begin{array}{l}(d-a\gamma )A{}_{\text{w}}=a\gamma A{}_{\text{c}}(14)\\ \text{则}:\gamma =\frac{d}{a}\frac{A{}_{\text{w}}}{A{}_{\text{w}}+A{}_{\text{c}}}=\eta {}_1\eta {}_2(15)\end{array}$

　　 将式 (15) 和高宽比λ=H/a代入式 (13) 得:

　　 $\zeta =1+\frac{1.875\eta {}_1\eta {}_2}{\lambda {}^2+3.75\eta {}_1^2\eta {}_2^2}(16)$

　　 式 (16) 是结构顶部楼层的扭转位移比计算公式, 为了对整体结构不同楼层扭转位移比的变化情况进行全面判断, 引入悬臂构件在集中荷载下的挠曲函数:

　　 $y=\frac{F{\rm H}{}^3(3-z)z{}^2}{6E{\rm I}}(17)$

　　 式中z为楼层所在高度与结构总高度的比值, 0<z≤1。

　　 则任意楼层处的转角为:

　　 $\phi =\frac{{\rm T}{\rm H}z}{G{\rm I}{}_{\text{Ρ}}}=\frac{F\gamma a{\rm H}z}{G{\rm I}{}_{\text{Ρ}}}(18)$

　　 将式 (17) , (18) 引入前述推导过程, 重新推导后, 得到扭转位移比的表达式为:

　　 $\zeta =1+\frac{1.875\eta {}_1\eta {}_2}{\frac{(3-z)z}{2}\lambda {}^2+3.75\eta {}_1^2\eta {}_2^2}(19)$

　　 由式 (19) 可见, 结构在地震作用下的扭转位移比仅与4个参数有关, 即核心筒的相对偏移率、核心筒面积比、结构的高宽比以及所考察楼层的相对位置。

　　 结构的周期由刚度和质量共同决定, 假定结构Y向平动刚度为K, 总质量为M, 未偏置结构的Y向平动周期为:

　　 ${\rm T}=2\text{π}\sqrt{{\rm M}/{\rm K}}(20)$

　　 核心筒向右发生偏置后, 结构Y向刚度沿X向的分布发生变化, 质心处的刚度变小。因此偏置后, 结构的Y向平动带有一定扭转效应, 对应的周期可能会增加。在计算该周期T′时, 应采用质心处的等效刚度K′, 该刚度可由质心位移反算。

　　 ${{\rm T}}^{\prime }=2\text{π}\sqrt{{\rm M}/{{\rm K}}^{\prime }}(21)$

　　 质心平动位移为:

　　 $u^{\prime }=u+\phi e=\frac{F{\rm H}{}^3}{3E{\rm I}}+\frac{F\gamma {}^{2}a{}^2{\rm H}}{G{\rm I}{}_{\text{Ρ}}}(22)$

　　 等效刚度与初始刚度之比为:

　　 $\frac{{\rm K}}{{{\rm K}}^{\prime }}=\frac{u^{\prime }}{u}=1+\frac{3.75\eta {}_1^2\eta {}_2^2}{\lambda {}^2}(23)$

　　 Y向平动周期的相对变化为:

　　 $\frac{{{\rm T}}^{\prime }}{{\rm T}}=\sqrt{\frac{{\rm K}}{{{\rm K}}^{\prime }}}=\sqrt{1+\frac{3.75\eta {}_1^2\eta {}_2^2}{\lambda {}^2}}>1.0(24)$

　　 即偏置后结构的实际平动周期会增大。

　　 考虑转动惯量J基本不变的情况下, 扭转周期的变化将主要取决于扭转刚度的改变。在前述基本假定下, 核心筒在X向发生偏置后, 绕X轴的惯性矩将不发生改变, 绕Y轴的惯性矩的两个组成部分 (外框柱项+核心筒项) 均发生变化, 根据移轴公式, 二者均呈增大趋势, 核心筒偏置后总惯性矩I_y′为:

　　 ${\rm I}{}_{{\text{y}}^{\prime }}={\rm I}{}_{\text{y}}+A{}_{\text{c}}e{}^2+A{}_{\text{w}}(d-e){}^2(25)$

　　 核心筒偏置后极惯性矩I_p′为:

　　 $\begin{array}{l}{\rm I}{}_{{\text{p}}^{\prime }}={\rm I}{}_{\text{x}}+{\rm I}{}_{\text{y}}+A{}_{\text{c}}e{}^2+A{}_{\text{w}}(d-e){}^2\\ =2{\rm I}+A{}_{\text{c}}e{}^2+A{}_{\text{w}}(d-e){}^2(26)\end{array}$

　　 式中:I_x为核心筒偏置前结构绕X轴的惯性矩;I_y为核心筒偏置前结构绕Y轴的惯性矩。

　　 核心筒偏置前后结构扭转周期的计算公式为:

　　 $\begin{array}{l}{\rm T}{}_{\text{θ}}=2\text{π}\sqrt{J/{\rm K}{}_{\text{θ}}}(27)\\ {\rm T}{}_{{\text{θ}}^{\prime }}=2\text{π}\sqrt{J/{\rm K}{}_{{\text{θ}}^{\prime }}}(28)\end{array}$

　　 式中:T_θ为核心筒偏置前的结构扭转周期;T_θ′为核心筒偏置后的结构扭转周期;K_θ为核心筒偏置前的结构扭转系数, K_θ=GI_p/H;K_θ′为核心筒偏置后的结构扭转系数, K_θ′=GI_p′/H。

　　 核心筒偏置后的周期相对变化为:

　　 $\begin{array}{l}\frac{{\rm T}{}_{{\text{θ}}^{\prime }}}{{\rm T}{}_{\text{θ}}}=\sqrt{\frac{{\rm K}{}_{\text{θ}}}{{\rm K}{}_{{\text{θ}}^{\prime }}}}=\sqrt{\frac{G{\rm I}{}_{\text{p}}/{\rm H}}{G{\rm I}{}_{{\text{p}}^{\prime }}/{\rm H}}}=\sqrt{\frac{{\rm I}{}_{\text{p}}}{{\rm I}{}_{{\text{p}}^{\prime }}}}\\ =\sqrt{\frac{2{\rm I}}{2{\rm I}+A{}_{\text{c}}e{}^2+A{}_{\text{w}}(d-e){}^2}}<1.0(29)\end{array}$

　　 由式 (29) 可知, 当核心筒出现偏置后, 相对原对称结构, 扭转刚度变大, 扭转周期将变短, 又由2.3.1节中结果可知垂直于偏置方向的平动周期变长, 因此最终结构的扭转周期比T_θ′/T′将变小。

　　 采用ETABS软件建立了共计24个钢筋混凝土框架-核心筒结构的数值计算模型, 研究了核心筒偏置程度、结构高宽比及采用何种补强措施等因素对于核心筒偏置结构受力性能的影响。各计算模型参数设定情况如表2所示, 各模型平面类型编号所对应的平面布置形式如图3所示。由于框架-剪力墙结构的各层刚度中心位置实际上并无明确的定义^[12], 因此本文采用核心筒的偏置程度来表征结构偏置水平的大小。平面形式A～F的偏置程度依次增大, 平面形式Cc, Dc, Ec是在平面形式C, D, E的基础上增设一排内柱得到的。

　　 所有计算模型的结构平面均为54m×54m的正方形, 核心筒平面为24m×24m的正方形。框架柱截面为1 000mm×1 000mm, 外框梁截面为300mm×1 000mm, 内框梁截面为300mm×900mm, 核心筒剪力墙外墙肢厚度为800mm, 内墙肢厚度为500mm;墙、柱的混凝土强度等级为C60, 梁、板的混凝土强度等级为C30;框架梁柱之间为刚接, 框架梁与核心筒之间为铰接。为避免不必要的变量对研究结果产生干扰, 本文的计算模型所有竖向构件沿结构全高度均未改变截面尺寸和材料。结构各层层高均为4.5m。结构分析时考虑竖向重力荷载及水平地震作用 (7度, 0.10g) , 楼面均布恒载2.5kN/m², 均布活载3.5kN/m²。

　　 分别计算各模型自振周期及振型, 结果见表3。计算结果表明, 在平面布置相同 (即结构偏置程度和层抗侧刚度相同) 时, 结构的高度越高, 则扭转周期比越小。结构高度不同时, 偏置程度对扭转周期比的影响程度不同, 高度较高时偏置程度对扭转周期比的影响较小;高度较小时偏置程度对扭转周期比的影响较大。偏置程度增大时, 虽然结构的扭转周期比会减小, 但是扭转成分在第1阶平动振型中的占比会增大, 因而不能错误地认为偏置程度增大能够降低扭转周期比从而减弱结构平扭耦合的程度。从有内柱模型与无内柱模型的比较中可以看出, 是否增设一列内柱对于结构的自振周期及扭转周期比几乎没有影响。

　　 分别计算各模型在规定水平力作用下的扭转位移比 (考虑5%的偶然偏心) 。偏置程度和结构高度对扭转位移比的影响结果如图4所示。核心筒偏置程度的增大会显著增大结构扭转位移比, 两者之间大致为线性关系。在结构平面布置相同时, 结构高度较小的模型相对于结构高度较高的模型具有更大的扭转位移比。这一现象在徐培福等^[13]的著作中亦有提及。但应注意, 这一现象并不意味着结构高度的增加可以减弱结构的扭转效应, 而是由于结构高度增加时, 结构平动位移增大的幅度大于结构扭转变形增大的幅度, 从而导致扭转位移比表现出了减小的趋势。在本文考察的高宽比范围内 (2～4) , 相对于偏置程度对扭转位移比的影响而言, 结构高度对结构扭转位移比的影响并不明显。

　　 结构高度约为200m的模型M200_A～M200_F的扭转位移比沿楼层变化情况如图5所示, 结构扭转位移比沿楼层从上至下逐步增大。造成该现象的原因主要在于结构底层平动位移很小, 从而导致扭转位移比相对较大。

　　 计算结果显示, 此类核心筒偏置结构在偏置程度较大时, 将表现出显著扭转效应, 极易在结构底层产生较大扭转位移比。若未采取相应的补强措施, 则此类结构下部楼层的扭转位移比极易超过规范限值。通过增设内柱的方式, 可以显著地减小结构的扭转位移比。在建筑功能与方案许可的情况下, 此类结构可考虑通过增设内柱来减弱结构的扭转效应。

　　 附加扭矩将会导致靠近核心筒一侧的外框柱剪力减小, 而远离核心筒一侧的外框柱剪力增大。结构外框柱、剪力墙编号如图6所示。水平荷载下不同偏置程度时200m高度模型典型外框柱的剪力如图7所示 (模型M200_F由于核心筒偏置过大, 增加了内柱, 对构件内力存在较大影响, 故仅用于整体比较, 不参与构件内力比较) 。外框柱最大剪力出现在结构顶层, 最大剪力值随偏置程度的增大变化不大;剪力变化幅度最大的部位为结构底层。

　　 在核心筒偏置时, 距离结构平面边缘较近一侧的核心筒剪力墙墙肢剪力将会减小, 而距离结构平面边缘较远一侧的核心筒剪力墙墙肢剪力将会增大。水平荷载下不同偏置程度时200m高度模型典型核心筒剪力墙墙肢的剪力如图8所示。

　　 本文通过理论分析及数值模型计算, 研究了核心筒偏置的高层建筑结构在水平地震作用和竖向重力荷载作用下的受力特点, 并得到以下结论:

　　 (1) 结构平面相同时, 结构高度越高扭转周期比越小;结构高度不同时, 偏置程度对扭转周期比的影响程度不同, 高度较高时偏置程度对扭转周期比的影响较小;高度较小时偏置程度对扭转周期比的影响较大;增设内柱对于结构的自振周期及扭转周期比几乎没有影响。

　　 (2) 核心筒偏置程度的增大会显著增大结构扭转位移比, 两者之间大致为线性关系。在结构平面布置相同时, 结构高度较小的模型相对于高度较高的模型具有更大的扭转位移比。