轻型折叠网壳房屋是一种广泛应用于工程实际的野营房屋, 如图1所示。此类房屋由轻质材料构成且表面气动特性十分复杂, 属典型的风敏感结构, 故风荷载成为房屋分析和设计的控制荷载之一。在满足房屋使用功能要求的前提下, 如何减少其受到的风荷载作用, 是这类房屋设计的关键。因此为了改善复杂体型折叠网壳房屋的抗风性能, 使其在风荷载作用下具有合理的外形, 亟需对轻型折叠网壳房屋进行基于抗风设计的外形优化研究。

　　 对于建筑物在风荷载作用下的外形优化, 国内外学者已进行了一定研究。Y.Ozmen^[1]采用风洞试验与数值模拟的方法, 分析了屋面坡度对双坡房屋表面风压分布的影响规律。严正林等^[2]对7种截面形式的高层建筑模型进行了气动外形优化风洞试验, 以建筑风力系数平均值与均方根值为优化目标, 分析了削角和凹角的改变对建筑风荷载的影响。但目前的研究仍存在不足之处, 目前研究主要集中在对沿海地区永久性房屋的研究上, 且研究对象体型较为简单, 对复杂体型的建筑如轻型折叠网壳房屋等的抗风优化研究较为缺乏。西北工业大学翼型研究中心^[3]对特定体型的野营折叠网壳房屋进行了风洞试验, 文献[4,5]运用数值模拟方法从理论上阐述了风速、风向角、开洞位置与大小对其风荷载体型系数的影响, 但是针对折叠网壳房屋外形优化的研究尚未深入开展, 理论研究滞后于工程应用。

　　 数值模拟方法具有许多优点, 如周期短、成本低、能够改变各种参数来研究其对结果的影响, 且不受试验干扰效应的影响。因此本文以风洞试验为基础, 建立数值风洞, 即利用计算机建立的虚拟风洞模型来模拟真实风环境。对多体型、多工况折叠网壳房屋进行优化设计, 得到具有良好抗风性能的合理外形, 对开发新型野营折叠网壳房屋具有较好的理论意义与工程应用价值, 同时也为类似轻型房屋抗风外形优化提供理论依据和设计方法。

　　 通过收集野营住房设备资料并统计其几何尺寸, 同时参考《空间网格结构技术规程》 (JG17—2010) ^[6], 在建筑满足排水、采光及其他使用要求的前提下选取合理的建筑模型参数, 采用无量纲的方法设计建筑模型, 根据国内外文献关于影响建筑物表面风效应尺寸参数的研究^[7,8,9], 将矢跨比、端门倾角、端门高选为优化参数, 选取端门倾角α为40°, 45°, 55°, 90°, 端门高h为0, H/4 (H为建筑高度) , 矢跨比H/B (B为建筑宽度) 为1/2, 1/3, 1/4, 2/3, 共计28种建筑模型, 如表1所示。表1中的方案00为原模型, 其矢跨比H/B=0.55, 端门倾角α=48°, 端门高h=H/4。在10m/s的风速下, 对房屋表面风场分别进行0°, 30°, 45°, 60°, 90°风向角下共计140种工况的风压分布数值模拟。风向角、风洞试验测点、房屋表面分区与几何尺寸的规定如图2所示。

　　 本文通过与风洞试验数据进行对比, 建立合理的数值风洞, 对所获得的数值解进行准确性和合理性验证, 确定轻型折叠网壳房屋在多体型、多工况下数值模拟的合理参数与关键技术。

　　 选取B类地貌风场, 风速为10m/s, 以0°风向角为例, 对不同关键参数下折叠网壳房屋模型数值风洞进行计算, 探讨与分析网格数量、离散格式、求解算法和湍流模型等参数和技术对计算结果的影响。网格单元数量选取70万、130万和200万三种, 离散格式选择二阶迎风格式和QUICK格式两种, 求解算法选择SIMPLEC, SIMPLE和PISO算法三种, 湍流模型选择标准k-ε模型、RNG k-ε模型、Realizable k-ε模型、标准k-ω模型和SST k-ω模型五种 (ε为耗散率) 。得到数值风洞各测点的风压系数, 对比相应测点的风洞试验数据, 其结果如图3所示。由图3分析可知, 在建立轻型折叠网壳房屋数值风洞时, 计算域的网格数量控制在130万左右、采用二阶迎风格式、SIMPLEC算法以及SST k-ω湍流模型对折叠网壳房屋的数值风洞模拟更合理、更精确, 其中, k表示湍动能, ω表示比耗散率。计算域尺寸、边界条件与收敛判定准则均参考文献[4]。

　　 图3 参数和技术对测点风压系数的影响

　　 对多体型、多工况的轻型折叠网壳房屋表面风压分布进行数值模拟计算, 得到建筑在多体型、多工况下的体型系数变化规律, 探讨与分析矢跨比、端门倾角、端门高和风向角等不同参数对折叠网壳房屋表面风压分布特性的影响, 为基于抗风设计的折叠网壳房屋外形优化奠定数据基础。

　　 折叠网壳房屋由两侧的端门与中间的网壳三部分组成, 其中端门部分主要由端门倾角α与端门高h两个端门参数决定, 端门对房屋表面风致响应影响效果显著, 根据数值计算结果分析端门参数对28种不同体型折叠网壳房屋风荷载体型系数的影响情况。

　　 以90°风向角为例进行分析, 体型系数以B区为界呈对称分布, 如图4所示。从图4可看出, 原模型方案00与其他体型相比, 在A3, B3, C3区均出现较大的负体型系数幅值, 且在A5, B6, C5区产生较大的正体型系数, 体型系数变化幅度较大且部分区域出现应力集中现象。端门倾角为90°时, A5与C5区出现有别于其他体型的较大负风压, 在建筑表面形成风吸力易造成风致破坏。在远离迎风面的区域端门倾角与体型系数变化呈负相关关系, 而在靠近迎风面的区域端门倾角与体型系数变化呈正相关关系, 且端门高为H/4时, 会有效缓解建筑表面风荷载, 因此综合各体型房屋表面体型系数可得, 端门倾角为45°且端门高为H/4的优化方案18的表面各分区体型系数较小且分布较为均匀, 可提高折叠网壳房屋的抗风能力。

　　 图4 不同端门参数下建筑表面各分区体型系数 (90°风向角)

　　 折叠网壳房屋中间的主体网壳主要由矢跨比H/B参数决定, 网壳作为房屋的主体结构, 对房屋表面风压分布的影响效果显著, 因此本节将根据数值计算结果分析矢跨比对28种不同体型折叠网壳房屋风荷载体型系数的影响情况。

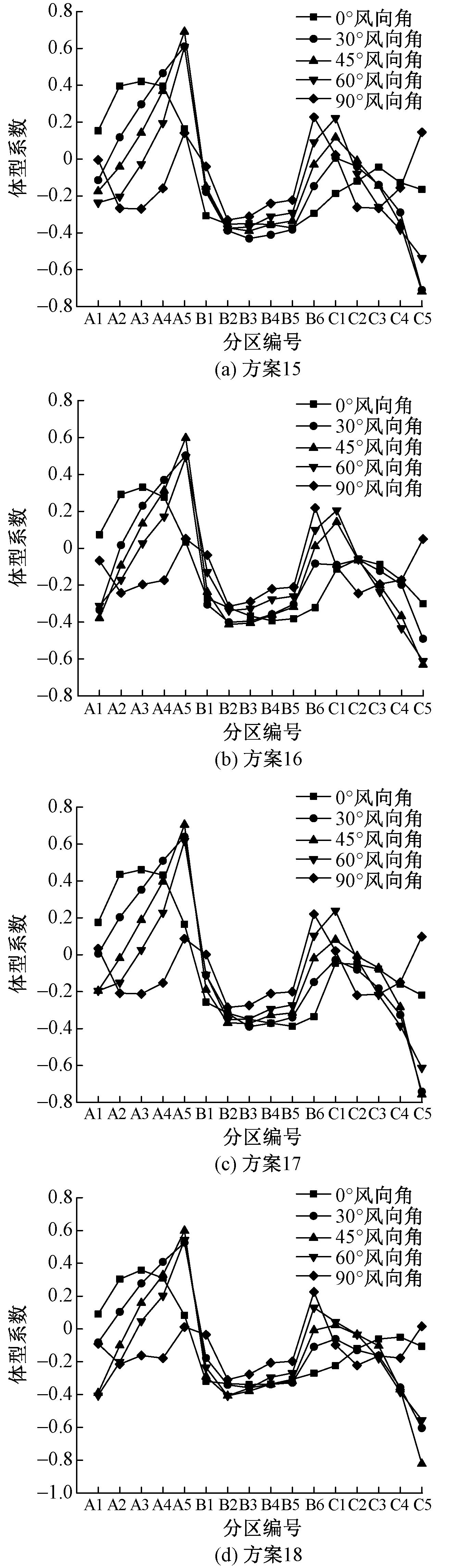
　　 以90°风向角为例分析, 不同矢跨比建筑表面各分区体型系数以B区为界呈对称分布, 变化趋势基本一致, 如图5～8所示。从图5～8可看出, 随着矢跨比的减小, 房屋各表面分区体型系数随之减小, 且风压系数分布更加均匀, 如图5 (b) 中矢跨比为1/4的优化方案16, 在A1, A3, B3, B6, C3风压较大的区域体型系数极值由原模型方案00的 (0.321, -0.606, -0.481, 0.538, -0.580) 降低为 (-0.067, -0.196, -0.290, 0.219, -0.194) , 最大降低幅度达79.1%。矢跨比为2/3时, 房屋会在A3与C3区出现非常高的负风压且变化幅度较大, 易造成房屋除迎风面和背风面之外的区域风致破坏, 而矢跨比为1/4时, 体型系数基本在-0.3～0.2间小范围波动, 变化幅度与极值均较小, 因此矢跨比的减小可有效提高折叠网壳房屋表面抗风性能。

　　 图5 不同矢跨比下建筑表面各分区体型系数 (α=40°)

　　  

　　 图6 不同矢跨比下建筑表面各分区体型系数 (α=45°)

　　  

　　 图7 不同矢跨比下建筑表面各分区体型系数 (α=55°)

　　  

　　 图8 不同矢跨比下建筑表面各分区体型系数 (α=90°, h=0)

　　  

　　 风向角对房屋表面风致响应具有十分显著的影响, 以具有较好抗风性能的矢跨比为1/4、端门倾角为40°与45°的建筑体型为例, 分析风向角对房屋表面风荷载分布的影响, 如图9所示。从图9可看出, 在0°与90°风向角下, 房屋的体型系数分布较为均匀且极值较小, 无明显的应力集中现象, 使折叠网壳房屋受风荷载的影响较小, 因此在进行房屋布置时可参考0°与90°风向角进行合理摆放。

　　 外形优化设计是通过建筑形体的自适应来降低房屋结构的风致响应, 通过对建筑形体的优化来化解房屋结构的不利风压分布, 使建筑形态与风环境相统一, 建筑表面风压分布均匀对房屋抗风设计更有利, 且风压变化幅度越小表明房屋表面应力集中现象越少且房屋受力越均匀合理, 而将分析体型系数标准差最小作为优化目标可有效反映建筑表面风压分布的均匀程度与风致响应。

　　 因此为了分析各方案在不同风向角下表面压力分布均匀程度并且保证折叠网壳房屋在风荷载作用下具有合理的外形, 本文以分区体型系数标准差为计算指标, 求得0°, 30°, 45°, 60°, 90°风向角下各方案体型系数标准差如图10所示。由图10分析可得, 在0°, 30°, 45°, 60°, 90°风向角下, 体型系数标准差最小的方案分别为优化方案18, 优化方案04, 优化方案20, 优化方案16, 优化方案19, 与原模型方案00表面体型系数标准差相比, 使原模型方案00在0°, 30°, 45°, 60°, 90°风向角下体型系数标准差由0.274, 0.379, 0.464, 0.424, 0.315减小为0.239, 0.236, 0.299, 0.270, 0.118。综合比较可知, 矢跨比H/B=1/4、端门倾角α=40°、端门高h=H/4的优化方案16与矢跨比H/B=1/4、端门倾角α=45°、端门高h=H/4的优化方案18体型系数标准差在各风向角下均较小。但是由我国《建筑结构荷载规范》 (GB 50009—2012) ^[10]中对于坡屋面积雪分布系数随坡度变化的规定可知, 屋面坡度越小越容易积雪, 故当端门倾角较小时, 端门部分因风力的搬运作用会形成积雪效应并存在雨水堆积的隐患, 端门倾角为40°的优化方案16端门部分坡度较缓, 易形成积雪与积水现象, 在使用时存在较大的不便与缺陷, 因此综合各风向角下折叠网壳房屋体型系数标准差与使用功能要求分析可得, 矢跨比H/B=1/4、端门倾角α=45°、端门高h=H/4的优化方案18在各风向角下表面风压分布较为均匀且极值风压较小, 风荷载对其表面风致响应影响较小且受力更为均衡, 有效提高了折叠网壳房屋的抗风性能, 故将具有更好抗风性能的优化方案18作为复杂体型折叠网壳房屋的体型最优方案。

　　 图10 不同风向角下各方案体型系数标准差

　　 为研究折叠网壳房屋体型优化方案在不同风向角下表面风压分布情况, 对比折叠网壳房屋原模型方案00与最优方案即矢跨比H/B=1/4、端门倾角α=45°、端门高h=H/4的优化方案18表面风压分布规律, 分别绘制0°, 30°, 45°, 60°, 90°风向角下原模型方案00与优化方案18的平均风压系数等值线分布图, 如图11～15所示。

　　 图11 0°风向角下优化方案00与优化方案18平均风压系数等值线图

　　  

　　 图12 30°风向角下优化方案00与优化方案18平均风压系数等值线图

　　  

　　 图13 45°风向角下优化方案00与优化方案18平均风压系数等值线图

　　  

　　 图14 60°风向角下优化方案00与优化方案18平均风压系数等值线图

　　  

　　 图15 90°风向角下优化方案00与优化方案18平均风压系数等值线图

　  

　　 将折叠网壳房屋的矢跨比降低到1/4、端门倾角降为45°且端门高取为H/4时, 折叠网壳房屋的抗风性能有了极大的改善与加强, 矢跨比的降低使主体网壳的跨度增加、坡度放缓, 气流在吹向主体网壳时爬升缓慢, 且在易发生气流分离的屋脊等分界处气流旋涡发育缓慢, 有效地降低了屋脊处的高负压区内风压极值与负压区的数量, 使主体网壳B区风压变化幅度明显减缓。来流风流向房屋时, 在屋面上风边缘发生流动分离的气流与上风角处分离的气流相叠加, 会形成锥形涡, 而矢跨比降为1/4后有效缓解了锥形涡的产生。将端门倾角降低为45°时, 既可以满足房屋排水与防积雪的使用功能要求, 又可以减缓来流在端门处的爬升速度, 可提升折叠网壳房屋的整体抗风能力。端门高取为H/4对房屋形成一个围挡, 可以对近地风起到较大的阻碍作用, 减弱来流风的风力。因此, 综合对比分析各种优化方案表面风压分布特性与体型系数变化可得, 经优化后矢跨比H/B=1/4、端门倾角α=45°、端门高h=H/4的优化方案18可明显降低折叠网壳房屋的风效应, 将房屋的风致响应降至最低, 极为有效地提高了房屋的抗风性能。

　　 综合对比28种折叠网壳房屋外形优化方案在0°, 30°, 45°, 60°, 90°风向角下表面各分区的体型系数、体型系数标准差与表面风压分布特性等目标参数, 分析可得矢跨比H/B=1/4、端门倾角α=45°、端门高h=H/4的18优化方案房屋有效提高了折叠网壳房屋抗风性能, 有利于房屋的抗风设计, 因此在进行折叠网壳房屋抗风设计时可参考表2所示的体型系数。

　　 (1) 经分析研究可知, 当数值风洞的计算域尺寸取为15L×8L×5L (其中L为房屋顺风向长度) 、采用二阶迎风格式、SIMPLEC计算方法、SST k-ω湍流模型与分区混合网格划分方案时, 数值计算的精度较高、稳定性较好且更为合理。

　　 (2) 综合对比分析各优化方案, 房屋表面各分区体型系数随着端门倾角α的减小而减小, 端门高h的增加可减小各分区体型系数的幅值。各分区体型系数随着矢跨比的减小而减小, 矢跨比的降低可加强气流在屋脊处的二次再附作用, 再附的气流为正压, 与屋面负压中和, 从而使风压减小, 在矢跨比降为1/4时, 房屋表面受风荷载影响较小且受力较为均匀。

　　 (3) 综合对比分析各优化方案, 迎风面风压系数均为正值, 主要受压力作用, 而背风面、侧面和屋顶由于受到气流旋涡作用, 其表面风压系数为负值且主要承受风吸力。风向角为30°, 45°, 60°时, 在发生气流分离的分区风压会产生较为明显的陡增和陡降现象, 而在风向角为0°和90°时房屋表面受风荷载影响较小, 使折叠网壳房屋抗风性能得以改善。

　　 (4) 以风压分布最均匀与体型系数标准差最小为优化目标对折叠网壳房屋进行合理外形优化分析, 得到当房屋矢跨比H/B=1/4、端门倾角α=45°、端门高h=H/4时的合理优化方案 (优化方案18) , 可有效化解房屋表面的不利风压分布, 体型系数标准差降低幅度达62%, 极大提高了折叠网壳房屋的抗风性能。建立合理的数值风洞能十分有效且经济地对多体型多工况下的建筑外形进行优化研究。