该项目位于贵阳市东部地区, 建筑功能为公寓和商业。总建筑面积20.2万m², 地上15.4万m², 地下4.8万m²。本工程地下室共3层, 地上部分由E, F, G三座塔楼和各自的裙房组成。塔楼与裙房连为一体, 裙房之间设防震缝, 各自形成独立的结构单元。因地下室在±0.000m标高以下9.4m范围内三面临空, 故各塔楼实际结构高度为建筑高度再加上9.4m。其中, E座塔楼地上25层, 结构高度为147.4m;F座塔楼地上51层, 结构高度为210.5m;G座塔楼地上29层, 结构高度为169.4m, 三座塔楼在立面上设有一次体型收进, 标准层平面尺寸均为36.6m×36.6m, 收进后平面尺寸均为28.4m×36.6m。裙房地上共3层, 结构高度为17.4m, 三个裙房在屋顶设连廊相连。整个项目建筑效果图如图1所示。

　　 三座塔楼1～3层主要功能为商业、餐饮、会议区, 层高5.1～6.0m。4层及以上各层均为公寓, 其中F座层高均为3.8m, E, G座层高均为5.5m。各楼座避难层层高同普通楼层层高。屋顶钢架层用于摆放室外设备。地上结构剖面见图2。地下室主要功能为车库和设备用房, 地下室四周三侧临土, 一侧临空, 临土部位设置垂直支护与土体隔离, 仅地下3层可以实现四周有土体嵌固, 故塔楼嵌固位置取在地下3层顶。场地下伏中风化岩体分布连续, 是理想的基础持力层, 主塔楼下采用筏板基础, 裙房和地库柱下采用独立柱基。地下结构剖面见图3。　　  

　　 三座塔楼均采用钢筋混凝土框架-核心筒结构体系, 楼面采用现浇混凝土梁板体系。其中F座属于超B级高度钢筋混凝土结构, G座属于B级高度钢筋混凝土结构。裙房采用钢筋混凝土框架结构体系。

　　 为形成塔楼立面的收进造型, 塔楼在顶部10层范围内核心筒进行收进, 从下层核心筒外墙上立柱承托上部结构重量。裙房之间的防震缝从地上3层到地下2层地面, 裙房之间的跨缝连桥在两端设置双向滑动的铰支座。裙房层和塔楼标准层结构平面布置如图4, 5所示。

　　 本工程结构设计使用年限为50年, 结构安全等级为二级, 抗震设防类别为丙类, 场地类别为Ⅱ类, 设计地震分组为第一组, 场地特征周期T_g为0.35s。抗震设防烈度为6度 (0.05g) , 阻尼比取0.05。基本风压为0.30kN/m² (按50年一遇) , 地面粗糙度类别为B类, 结构体型系数为1.4。

　　 F座外框柱采用截面为1 600×1 650～700×700, 核心筒外墙厚600～300mm, 核心筒内墙厚300～200mm。标准层楼板厚100mm, 避难层、机房层等底板加厚至150mm。框架柱及剪力墙混凝土强度等级从下往上为C60～C40, 梁板混凝土强度等级为C30。

　　 根据《超限高层建筑工程抗震设防专项审查技术要点》 (建质【2010】109号) , F座属于高度超B级、较规则超限高层建筑结构, 抗震性能目标定为C级, 结构设计性能指标见表1。

　　 分别采用SATWE和MIDAS Building对F座塔楼进行了整体弹性反应谱分析, 主要结果见表2。由表2可知, SATWE和MIDAS Building两种程序计算结果比较吻合, 周期、位移、剪重比等各项指标均满足规范的要求。

　　 在多遇地震和风荷载 (50年重现期) 作用下, 结构楼层剪力计算结果如图6所示, 楼层倾覆力矩计算结果如图7所示。由对比结果可见, F座塔楼结构设计为风荷载控制。

　　 采用程序SATWE对F座塔楼进行多遇地震弹性时程分析, 根据设防烈度、场地类别等条件选取两条天然波和一条人工波, 峰值加速度最大值调整至18gal, 地震波有效持续时间均超过35s, 大于5倍结构基本自振周期, 时间步长取0.02s。所选取三条地震波的平均地震影响系数曲线与振型分解反应谱法所用地震影响系数在主要振型的周期点上相差不大于20%, 满足抗规^[1]在统计意义上相符的要求。

　　 基底剪力计算结果见表3。由表3可知, 三条地震波作用下结构底部剪力与反应谱法计算结果比值均在65%～135%范围内, 其平均值与反应谱法计算结果亦在80%～120%范围内, 均满足规范要求。弹性时程分析的三组加速度时程的各楼层剪力与反应谱计算结果进行比较, X向为反应谱层楼层剪力的0.96～1.35倍, Y向为反应谱层楼层剪力的0.92～1.32倍。进行施工图设计时, 地震作用下各楼层剪力取弹性时程计算结果的包络值与反应谱计算结果的较大值。

　　 采用PKPM-SAUSAGE程序对F座塔楼进行了动力弹塑性时程分析。采用材料应力-应变层级的精细模型, 一维单元采用非线性纤维单元, 沿截面和长度方向分别积分。二维壳板单元采用非线性纤维分层单元, 沿平面内和厚度方向分别积分。楼板也按二维壳元模拟。钢材的动力硬化模型采用双线性随动硬化模型, 在循环过程中无刚度退化, 但考虑包辛格效应。混凝土材料模型采用弹塑性损伤模型, 可考虑材料拉压强度差异、刚度及强度退化、拉压循环裂缝闭合呈现的刚度恢复等性质, 不考虑截面内横向箍筋的约束增强效应。

　　 选取Ⅱ类场地 (T_g=0.40s) 的2组天然波 (天然波1, 2) 和1组人工波, 共3组地震波进行结构大震弹塑性时程分析。峰值加速度最大值调整至125gal, 地震波有效持续时间均超过35s, 时程波对应的加速度反应谱在结构各主要周期点上与规范谱相差不超过20%。地震波双向输入, 主次方向的地震波峰值比为1∶0.85, 结构初始阻尼比取5%。

　　 各组地震波作用下结构的基底剪力峰值、剪重比统计结果见表4, 结构最大楼顶位移、最大层间位移角及相应楼层统计结果见表5。由分析结果可见, 3组地震波产生的结构最大层间位移角为1/224, 小于规范的限值1/100, 满足规范“大震不倒”的要求。大震弹塑性时程下最大层间位移角约为小震弹性反应谱的5.1倍。大震弹塑性时程下基底剪力约为小震弹性反应谱的4.7倍。说明罕遇地震作用下结构进行了一定程度的塑性开展。

　　 本结构在人工波Y主方向作用下的反应最大, 图8给出了该组地震波作用下的各墙肢受压损伤情况。由图8可见, 核心筒大部分连梁的混凝土受压损伤因子超过0.5, 形成了塑性铰机制, 很好地发挥了屈服耗能的作用;核心筒主墙肢受压损伤部位主要集中在底部两层和竖向体型收进位置, 首层主墙肢局部区域轻度损伤, 2层以上核心筒各主墙肢总体保持弹性。设计中将对核心筒首层、2层以及收进层 (41层和42层) 主墙肢的配筋适当加强。

　　 在3组地震波X, Y主方向作用下, 大部分外框柱处于弹性状态, 仅少量外框柱出现轻度塑性损伤, 但尚未形成塑性铰。图9为人工波Y主方向作用下外框架柱受压损伤情况。结果表明, 外框架柱在大震作用下仍保持一定的承载能力, 能够起到抗震二道防线的作用。

　　 楼板体系是结构传递竖向荷载和水平荷载的重要组成部分, 也是连接核心筒和外框架柱之间的重要水平构件。在水平力作用下楼板体系需要确保结构整体受力、变形协调。

　　 本项目塔楼在竖直方向有两次体型收进, 分别位于3层顶和41层顶;考虑到该两处位置楼板在水平地震作用下传递较大水平剪力、协调结构空间变形, 将楼板加厚至150mm。采用PMSAP软件对整体结构进行中震作用下的楼板应力分析, 楼板在双向地震作用下主拉应力S11, S22与混凝土抗拉强度值进行比较 (C30, f_t=1.43MPa, f_tk=2.01MPa) , 根据分析结果对拉应力较大区域进行配筋构造加强, 分析结果如图10, 11所示。

　　 由图10, 11可见, 中震下3层顶和41层顶楼板的主拉应力最大值均小于混凝土轴心抗拉强度f_t, 3层顶楼板在双向地震作用下主应力峰值出现在主裙楼交接的位置。41层顶楼板在双向地震作用下主应力峰值出现在核心筒周边及局部开洞位置。在应力集中的区域, 考虑采用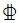10@200双层双向通长附加配筋以抵消拉应力。

　　 传统的结构分析方法仅考虑正常使用阶段荷载情况对主体结构的作用, 未考虑施工阶段荷载工况和加载顺序对结构的影响, 并且忽略了混凝土在长期荷载下收缩和徐变效应。上述因素将会导致传统分析方法的计算结果与实际结构效应存在相当大的差异。而超高层建筑竖向构件的变形差异会导致水平梁板构件产生明显的附件内力, 过大的变形差也将导致楼板倾斜、幕墙变形、隔墙开裂等一系列影响正常使用功能的问题^[2]。因此, 对超高层建筑进行施工阶段和后期使用阶段结构变形进行模拟分析很有必要。

　　 混凝土时变模型采用CEB-FIP1990模型^[3], 模型考虑混凝土特征强度、构件尺寸、水泥种类、环境相对湿度、加载龄期、持续时间等因素来预测结构的收缩、徐变效应。混凝土在龄期t₀时开始受到应力σ_c (τ) (t₀≤τ≤t) 作用, 在龄期t时混凝土产生的总应变由弹性应变ε_ci (t) 、徐变应变ε_cc (t) 和收缩应变ε_cs (t) 三部分组成。

　　 $\begin{array}{l}\epsilon {}_{\text{c}\text{i}}(t)=\frac{1}{E{}_{\text{c}}(t)}\left[\sigma {}_{\text{c}}(t{}_0)+{\displaystyle \int }{}_{t{}_0}^t\frac{\partial \sigma {}_{\text{c}}(\tau )}{\partial \tau }\text{d}\tau \right](1)\\ E{}_{\text{c}}(t)=E{}_{\text{c}\text{i}}\sqrt{\text{e}{}^{s(1-\sqrt{28/t})}}(2)\end{array}$

　　 式中:E_ci为混凝土28d时的弹性模量;E_c (t) 为龄期t时混凝土的平均模量;s为水泥种类系数。

　　 $\epsilon {}_{\text{c}\text{c}}(t)=\text{ϕ}(t,t{}_0)/E{}_{\text{c}\text{i}}\left[\sigma {}_{\text{c}}(t{}_0)+{\displaystyle \int }{}_{t{}_0}^t\frac{\partial \sigma {}_{\text{c}}(\tau )}{\partial \tau }\text{d}\tau \right](3)$

　　 式中ϕ (t, t₀) 为混凝土随时间变化的徐变系数。

　　 $\epsilon {}_{\text{c}\text{s}}(t,t{}_{\text{s}})=\epsilon {}_{\text{c}\text{s}0}\beta {}_{\text{s}}(t-t{}_{\text{s}})$

　　 式中:ε_cs0为混凝土名义收缩系数;t_s为考虑收缩开始时混凝土龄期;β_s (t-t_s) 为与时间相关的收缩变化发展系数。

　　 采用MIDAS Gen软件分别对E, F, G三座塔楼进行施工加载验算, 考虑混凝土受荷与收缩开始龄期t₀为3d, 环境相对湿度为70%, 水泥种类常数S为0.25 (普通水泥) , 施工期间恒荷载考虑结构自重和建筑做法、隔墙、幕墙等各项附加恒荷载, 施工活荷载按照1kN/m²考虑, 使用期间活荷载在结构封顶后施加。施工期间, 外框柱和核心筒同步施工, 每一层为一个施工步, 每一步持续10d。为分别研究框架核心筒结构外框柱与核心筒墙体的竖向变形, 选取F座塔楼外框柱Z1和核心筒剪力墙Q1, 位置如图5所示。

　　 图12为F座塔楼在一次性加载与施工模拟加载两种条件下Z1和Q1各层节点的位移图。计算结构暂不考虑收缩、徐变等材料时变效应。由图12可知, 在一次性加载条件下, Z1和Q1各层节点的位移随着楼层数的增加而曲线上升, 在最高层达到最大值。在施工模拟加载条件下, Z1和Q1各层节点的位移随着楼层数的增加先增加后减小, 最大的竖向位移在结构中部偏上的位置。考虑到施工模拟加载条件下, 竖向构件的变形为施工后变形, 施工前的变形已经根据设计图纸得到调平补偿。Z1在1～25层施工模拟加载下的竖向位移略大于一次性加载下的竖向位移, 25层以上各层施工模拟加载下的位移开始远小于一次性加载下的位移。Q1各层在施工模拟加载下的竖向位移均小于一次性加载下的位移。一次性加载和施工模拟加载的计算结果在竖向构件的竖向变形上存在很大的差异, 由此导致结构的内力分布也将有很大的不同。因此, 有必要根据结构实际的施工顺序进行加载计算。

　　 在结构施工过程中, 混凝土强度和压缩模量等材料特性跟施工进程紧密相关, 混凝土成型后, 其收缩徐变等效应也随着施工进程不断变化。图13为考虑混凝土时变效应的施工模拟加载结果。

　　 从图13可以看出, 在施工加载过程中, 考虑混凝土的时变效应情况下, 竖向构件的竖向变形量为分别考虑其弹性压缩量、徐变量、收缩量的总和, 从统计结果来看, 收缩量占比最小, 徐变量次之, 弹性压缩量最大, 竖向变形的总和约为弹性压缩量的2.0～2.3倍, 因此, 混凝土的收缩、徐变效应在竖向构件变形计算中不可忽视。

　　 为减小竖向构件变形对建筑物正常使用功能的影响, 建议在施工前期进行考虑时变效应的施工模拟加载验算, 计算出各层主要竖向构件的施工后总压缩量, 在施工过程中对每层的竖向构件顶标高进行预调整, 控制每层竖向构件顶标高为设计标高和施工后期总压缩量之和。以Z1和Q1为例, 各层顶施工后期总压缩量即为图13给出的结果。

　　 外框柱与核心筒结构形式不同, 受荷范围不同, 其竖向变形必然有所差异, 如果差异过大将导致外框柱与核心筒之间楼板开裂, 与之相连的框架梁产生较大的附加内力。图14为Z1与Q1的施工阶段的竖向变形差, 其中包含了混凝土的弹性压缩变形、徐变、收缩等因素。由图14可以看出, Z1与Q1在收缩量上基本一致, 二者差值约为零。变形差总和主要由压缩变形和徐变因素导致。变形差的最大值出现在32层, 最大值为36.4mm, 其中弹性压缩变形差为20.4mm, 徐变变形差为16mm。

　　 常规设计软件施工模拟计算可以考虑竖向构件的弹性压缩变形, 而竖向构件的徐变变形差通常无法反应, 与外框柱和核心筒相连的框架梁由于竖向构件徐变变形差导致的端部附加内力可由式 (1) 计算, 据此对框架梁局部配筋进行相应加强:

　　 ${\rm M}=\frac{6B{}_l\Delta {}_{\text{n}}}{L{}_{\text{n}}^2},V=\frac{2{\rm M}}{L{}_{\text{n}}}(1)$

　　 式中:M为梁端附加弯矩;V为梁端附加剪力;B_l为混凝土长期刚度;Δ_n为竖向构件考虑徐变后的变形差;L_n为梁净跨。

　　 按照式 (1) 对位于32层的核心筒与外框柱之间的某框架梁进行计算, 得框架梁在核心筒一端附加负弯矩约183kN·m, 附加剪力约41kN, 由此在该梁端附加上铁225。据此原则, 其余楼层核心筒 与外框柱之间框架梁则根据其实际竖向构件徐变位移差增设相应的配筋量。

　　 对贵阳某超高层塔楼的结构设计进行了整体介绍。针对其超限特点, 提出了抗震性能目标及其加强措施。运用多程序对抗震计算结果进行比较分析, 补充弹性时程计算和静力弹塑性分析, 确保抗震计算可靠性。对整体结构进行考虑混凝土时效的施工模拟验算, 针对竖向构件的变形量进行分析, 提出了相应的设计思路和计算方法, 有效地保证了结构整体的安全性。