扩展基础的冲切破坏是指在基础板的弯剪区域先出现斜裂缝, 斜裂缝不断向上扩展, 最后柱连同一个冲切锥与基础板脱离, 此时弯曲钢筋没有屈服, 破坏非常突然且毫无征兆, 破坏前没有形成一个完整的屈服机构, 属于脆性破坏, 造成的后果非常严重。因此, 在对扩展基础进行设计时, 首先要对其抗冲切性能进行研究。

　　 然而, 目前国内外对基础的抗冲切研究主要是针对钢筋混凝土矩形柱, 对异形柱的研究甚少, 但随着混凝土结构高度的增加, 矩形柱的截面面积不断增大, 在纵横墙交接处由于柱的宽度远大于墙体的厚度, 影响房间美观、不利于家具摆放等一系列问题不断凸显。因此L形、T形、十字形柱越来越受到设计师的青睐, 我国也陆续出台了相关标准来对其进行规范, 如《混凝土异形柱结构技术规程》 (JGJ149—2006) ^[1] (简称异形柱规程) 等。但是, 我国《建筑地基基础设计规范》 (GB 50007—2011) ^[2] (简称地基规范) 及异形柱规程并没有明确规定异形柱对基础及楼板的冲切性能的影响, 美国规范ACI 318-08^[3]、欧洲规范EN 1992-1-1∶2004^[4]和英国规范BS 8110^[5]虽然对十字形柱的冲切临界周长进行了规定, 但是并未对L形、T形柱的冲切临界周长进行说明。设计人员在对异形柱下扩展基础进行设计时只能凭借经验或将其等效为等面积的矩形柱进行计算, 这势必会与实际结果存在较大的误差。鉴于上述情况, 本文借助MSC.Marc有限元软件首先对某矩形柱扩展基础试验模型进行精细化有限元模拟, 并将模拟结果与试验结果进行对比。在确保建模方法正确的前提下, 对3种典型异形柱 (十字形、T形和L形) 下扩展基础进行建模分析得到其冲切破坏形态及冲切承载力, 并采用美国规范ACI318-08^[3]规定的冲切承载力的计算公式结合文献[6]中的冲切临界周长公式对模型的冲切承载力进行计算, 最后综合对比99个矩形柱基础的各国规范公式计算结果和试验结果, 证明了本文异形柱基础的数值模拟方法和冲切承载力计算方法均是正确的, 可以为工程设计提供参考。

　　 本文选用文献[7]中试验的某矩形柱下扩展基础作为MSC.Marc软件的模拟对象, 基础板截面尺寸为1 450mm×1 050mm, 板厚为220mm, 柱截面尺寸为250mm×250mm, 实测混凝土强度和钢筋强度分别为38.3MPa和370MPa, 基础的配筋情况如图1所示, 基础板配筋率为0.36%。

　　 建模时混凝土结构采用实体Soild单元模拟, 钢筋采用Truss单元模拟, 钢筋通过MSC.Marc软件中的Insert命令嵌入到混凝土结构中。由于土与结构相互作用极为复杂, 且本文的研究对象为基础的冲切破坏性能, 因此建模时做如下简化处理:在加载过程中, 将柱顶部固定, 将试验得到的基底反力分布模式施加到基础板底面上, 以模拟地基对基础的作用。

　　 混凝土本构关系采用E.Hognestad^[8]提出的本构关系计算公式 (1) 进行定义, 屈服准则选用软件MSC.Marc中的Buyukozuturk准则, 运用该准则进行计算时需将混凝土的应力-应变关系转换为等效应力-等效塑性应变关系^[9]。

　　 式中:ε₀为峰值应力σ₀所对应的应变, 取ε₀=0.002;峰值应力σ₀=0.85f_c', 其中f_c'为混凝土圆柱体抗压强度;ε_u为破坏时的应变, 取ε_u=0.003 3。

　　 钢筋本构关系采用理想弹塑性本构模型———双线性本构模型^[10], 其计算公式见式 (2) , 屈服准则采用von Mises屈服准则, 强化准则采用随动强化。

　　 式中ε_y为钢筋屈服应变, ε_y=f_y/E_s。

　　 基础板的挠度f按公式 (3) 进行计算:

　　 式中:L_短为基础短边尺寸;H1~H4, H1'~H4'分别为测点1~4, 1'~4'的竖向位移, 各测点位置如图2 所示。

　　 数值模拟与试验得到的荷载-挠度曲线对比如图3所示。从模拟得到的基础荷载-挠度曲线可知, 当荷载增加至733k N时, 曲线出现明显的拐点, 代表基础已基本破坏, 随后挠度急速增加但荷载增幅较小。这与试验观察到的“基础板的挠度在加载到750k N时出现大蝠增加, 基础板的裂缝开展迅速, 板的变形加快”^[7]这一现象基本吻合。从试验曲线和模拟曲线整体对比可以发现, 在相同荷载作用下, 数值模拟得到的基础挠度要比试验挠度略小, 其原因可能是由于Insert命令是直接将钢筋嵌入到混凝土单元中, 未考虑到两者的粘结滑移作用, 导致模型的刚度变大, 变形较小, 但曲线整体变化趋势与试验曲线吻合得较好。

　　 图4~7为加载至150步、160步、170步、180步的等效开裂应变云图, 荷载步对应的荷载分别为539, 600, 667, 733k N。由图可知, 裂缝首先出现在沿长度方向的基础板底面 (图4) ;随着荷载的继续增加, 裂缝逐渐向外、向上扩展 (图5, 6) ;当加载至733k N时裂缝延伸至柱根部, 中心锥体下陷, 逐渐与四周脱离, 发生冲切破坏 (图7) 。图8为试验体试验时的最终破坏形态和数值模拟得到的破坏时的等效开裂应变云图, 对比可知, 两者的破坏状态基本一致。

　　 本文对十字形、L形和T形3种典型柱截面扩展基础进行数值模拟, 根据异形柱规程对柱截面进行配筋, 配筋情况如图9所示。图中未标注的纵向钢筋为816, 纵筋配筋率为1.15%, 箍筋为8@100, 体积配箍率为1.42%。混凝土强度等级为C30, 基础板尺寸均为1 300mm×1 300mm, 板厚及异形柱高度均为500mm, 板底双向配置钢筋16@150, 配筋率为0.27%。

　　 通过数值模拟得到的3种异形柱下扩展基础的荷载-挠度曲线如图10所示。由图可知, 十字形柱、T形柱和L形柱扩展基础的冲切承载力分别为3 128, 2 999, 2 958k N, 且3种异形柱扩展基础均是在较小挠度下就发生冲切破坏, 破坏时几乎没有发生明显的塑性变形, 比较突然, 呈现明显的脆性破坏特征。三者在达到冲切承载力时的等效开裂应变云图见图11~13。模拟显示, 在柱截面尺寸及配筋率相同的情况下, 十字形柱的承载力较高, 破坏程度较小。

　　 本文采用美国规范ACI 318-08^[3]规定的基础冲切承载力计算公式对3种异形柱基础的承载力进行计算, 计算公式如下:

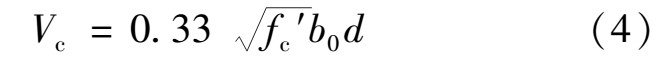
　　 式中:f_c'为混凝土圆柱体抗压强度;d为受压纤维最外缘到板内受拉钢筋形心的距离, 相当于我国地规中截面的有效高度h₀;b₀为冲切临界周长, 其中十字形柱临界周长按美国规范ACI 318-08^[3]的规定进行取值, 由于国内外规范中并没有明确规定L形柱和T形柱的冲切临界周长的取值方法, 因此本文按照文献[6]中的方法对L形柱和T形柱的临界周长u_m进行计算, 3种异形柱基础的冲切临界周长均为u_m=u₀+4h₀, 计算简图如图14所示。

　　 表1为冲切承载力V_c数值模拟结果与计算结果的对比。可见十字形柱、T形柱、L形柱基础的冲切承载力模拟结果分别是计算结果的1.21倍、1.12倍和1.09倍。文献[11]采用3种规范 (即中国地基规范, 美国规范ACI 318-08^[3], 欧洲规范EN 1992-1-1∶2004^[4]) 对99个矩形柱下扩展基础试验体的冲切承载力进行计算, 试验结果与计算结果的比值如表2所示。从表2中可知, 对于矩形柱下基础的冲切承载力, 中国地基规范与美国规范ACI 318-08^[3]计算结果较为接近, 试验值分别为计算值的1.25倍和1.21倍。通过表1和表2的对比可知, 异形柱下扩展基础的冲切承载力模拟结果比计算结果偏大是合理的。因此可以采用本文的数值模拟方法对异形柱下扩展基础的冲切性能进行深入研究。

　　 (1) 详细介绍了采用MSC.Marc有限元软件对矩形柱扩展基础冲切破坏的模拟过程, 通过与试验结果的对比分析可知, 两者的荷载-挠度曲线吻合较好, 模型的冲切破坏过程与试验现象基本一致。

　　 (2) 对3种异形柱 (十字形、T形和L形) 扩展基础的冲切破坏进行数值模拟, 并采用美国规范ACI 318-08^[3]中的冲切承载力计算公式结合文献[6]中的冲切临界周长公式对模型的冲切承载力进行计算, 结果表明, 异形柱下扩展基础的冲切承载力模拟结果比计算结果偏大。结合对99个矩形柱基础的各国规范公式计算结果和试验结果进行的对比分析, 证明了本文的异形柱基础的数值模拟方法和冲切承载力计算方法的可行性。

　　 本文的研究成果为工程设计提供参考的同时, 也可采用该成果对异形柱扩展基础的冲切破坏机理进行深入分析, 从而对冲切承载力计算公式做进一步修正。