现浇混凝土弧形梁结构设计分析
0 引言
随着国内经济的飞速发展, 现如今各种建筑形式层出不穷, 新颖、独特的建筑造型也是风格迥异, 弧形窗、弧形阳台、弧形转角等形式的造型决定了结构中弧形梁构件的出现。弧形梁的计算在结构设计中是一大难点, 受力较为复杂, 因为弧形梁不同于直线梁, 在竖向荷载作用下, 不仅产生弯矩、剪力, 还会产生扭矩[1]。本文通过弧形梁的理论计算分析以及与实际工程设计对比, 复核验算软件设计结果是否合理, 并提出软件设计中扭矩折减系数的参考取值, 以期得到较好的设计成果, 使结构符合实际的受力状态, 实现结构设计的“安全、适用、经济”目标。
1 弧形梁的内力计算
1.1 单跨无直线段圆弧梁内力计算
如图1所示, 单跨无直线圆弧梁的两端均按固定端考虑, 在均布竖向线荷载q的作用下产生跨中弯矩Mc、跨中剪力Vc以及跨中扭矩Tc, 分别按下式[2]计算:
图1 圆弧梁计算简图
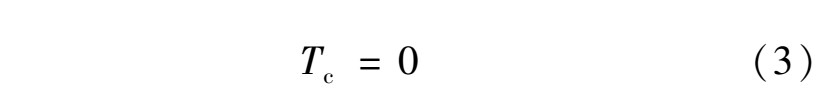
其中:
式中:θ为圆弧梁中心角的1/2;λ为截面的弹性常数, 其数值由EI/GJ计算, 其中EI为圆弧梁截面抗弯刚度, GJ为圆弧梁截面抗扭刚度, 也可通过查表1得出, 与圆弧梁的高度和宽度之比 (h/b) 相关;kc为一个参考系数[3], 取值与参数θ, λ相关。
根据圆弧梁中心角θ及λ的常用取值, 利用公式 (4) 计算得出kc值详见表2。
表1 λ取值
表2 kc计算值
任意截面的弯矩Mφ、剪力Vφ、扭矩Tφ按下式[2]计算:
式中:q为竖向均布线荷载, k N/m;φ为自圆弧对称轴位置线与任意位置截面处夹角, rad;R为圆弧梁的半径, m。
1.2 两端带直线段圆弧梁的内力计算
如图2所示, 两端带直线段圆弧梁一般用于跨度较大且框架柱设置受限的房屋边角部位, 受力形式比不带直线段的圆弧梁更为复杂, 计算时两端均按固定端考虑, 梁上有均布线荷载q及集中荷载Q作用。计算其内力时做如下假定[4]:1) 结构构件处于线弹性工作范围内;2) 构件截面整条轴线保持大小不变;3) 构件变形分析时略去剪切变形的影响;4) 材料泊松比μ=1/6;5) 截面的弹性常数λ=EI/GJ按表1取值计算。
如图2所示, 两端带直线段圆弧梁可分为三段 (DC, CB, BA段) 分别进行计算分析, 释放D点约束, 取该处弯矩、扭矩、剪力分别为MD, TD, VD, 各分段内力如下:
图2 两端带直线段圆弧梁计算简图
(1) DC段任意点X处截面 (图3) 的弯矩MX、剪力VX、扭矩TX按下式计算:
式中:MQ1, VQ1, TQ1为竖向集中荷载Q作用下梁点X处截面的弯矩、剪力、扭矩, 若无集中荷载作用则三者均取为0。
图3 DC段任意点X处截面内力计算简图
(2) CB段任意点X处截面 (图4) 的弯矩MX、剪力VX、扭矩TX按下式计算:
式中:MQ2, VQ2, TQ2为竖向集中荷载Q作用下梁点X处截面的弯矩、剪力、扭矩, 若无集中荷载作用则三者均取为0。
图4 CB段任意点X处截面内力计算简图
(3) BA段任意点X处截面 (图5) 的弯矩MX、剪力VX、扭矩TX按下式计算:
式中:r为BC梁段圆弧对应的半径;MQ3, VQ3, TQ3为竖向集中荷载Q作用下梁点X处截面的弯矩、剪力、扭矩, 若无集中荷载作用则三者均取为0。
图5 BA段任意点X处截面内力计算简图
2 实际工程案例应用与分析
2.1 工程概况
节能环保产业园工业地产项目位于长沙市国家级长沙高新技术产业开发区西侧, 规划有科研楼、加速器厂房、孵化器厂房、宿舍楼及配套用房。规划总建筑面积为319 545.19m2, 地下建筑面积为57 220.69m2。其中, 孵化器厂房中B-2#栋建筑为风车形外立面造型, 平面布置详见图6, 房屋四角及周边均为圆弧造型设计, 为了配合建筑线条设计弧形结构梁, ?/?轴交 (1) / (2) 轴的梁为单跨无直线段圆弧梁 (1/4圆, 半径为2.0m) , 截面尺寸为300×750, ?/?轴交 (5) / (7) 轴的梁为带一个直线段圆弧梁, 截面尺寸为350×750。采用软件PKPM, YJKS1.8建模计算时, 楼面均布恒荷载为1.8k N/m2, 均布活荷载为2.5k N/m2, 外边梁线性恒荷载为8.9k N/m, 弧形梁设计的扭矩折减系数默认值为1.0, 其余直线梁的扭矩折减系数为0.4, 提取软件PKPM, YJKS1.8计算值, 与本文公式计算值进行对比分析。
图6 B-2#栋建筑结构平面布置图
2.2 内力分析
对于(C)/(D)轴交 (1) / (2) 轴的单跨无直线段圆弧梁, 其弯矩、剪力及扭矩按本文公式计算结果及软件PKPM, YJKS1.8计算结果见表3。
表3 单跨无直线段圆弧梁不同计算方式计算的内力结果
注:按本文公式计算时, λ取值4.875, kc经查表2计算得kc=0.083 0。
对于(C)/(D)轴交 (5) / (7) 轴的带一个直线段圆弧梁, 其弯矩、剪力及扭矩按本文公式计算的结果及软件PKPM, YJKS1.8计算的结果见表4。
由表3和表4可见, 软件计算的弧形梁的弯矩、剪力、扭矩均偏大于本文理论计算值, 但相差不大, 其中圆弧端支座处扭矩理论计算值约为软件计算值的0.85倍, 说明结构设计软件PKPM, YJKS1.8在实际工程应用中是偏于保守的, 因此, 针对软件PKPM, YJKS1.8中弧形梁设计的扭矩折减系数默认值取为1.0, 本文建议该值可取0.85, 拟合真实受力情况进行结构设计。
表4 带一个直线段圆弧梁不同计算方式计算的内力结果
注:按本文公式计算时, λ取值3.802, kc经查表2计算得kc=0.083 3。
3 结论及建议
在实际工程计算中, PKPM及YJKS1.8软件对于弧形梁的扭矩折减系数默认值为1.0, 通过对弧形梁的理论分析计算与软件计算结果对比分析, 可知该取值偏于保守, 本文建议对于弧形梁的扭矩折减系数可取0.85。若同时考虑一侧楼板作为梁翼缘的有利作用时, 弧形梁抗扭计算中扭矩折减系数的取值还可进一步减小。这符合当前设计经济性与安全性相统一的特点。当软件的个别内力计算值与实际受力情况相差较大时, 建议按本文提供的理论表达式进行复核计算。
此外, 一般而言, 带直线段圆弧梁在估算其弯矩时, 可以通过与其轴线长度相等的直梁来代替, 由于弧形梁在水平面内的弯折从而使得弯矩的传递路径发生改变, 表现出支座处固端弯矩增大而梁底弯矩减小, 而这种增大与减小的幅度是与梁自身的抗扭刚度是成反比关系, 即抗扭刚度越大, 梁端和梁底弯矩的变化幅度越小, 弯矩分布越趋近于直线梁;带两个直线段圆弧形梁中弧形段较小 (即弧段半径不大于较长直线段的长度) 时, 可以忽略弧形段梁的影响, 而与水平折梁情况等同对待。
[2]龙驭球, 包世华.结构力学教程[M].北京:高等教育出版社, 1988:96-147.
[3]建筑结构静力计算手册编写组.建筑结构静力计算手册[M].北京:中国建筑工业出版社, 1995.
[4]孙训方, 方孝淑, 关来泰.材料力学 (上) [M].北京:高等教育出版社, 1989:179-184.