中风化砂页岩中抗浮锚杆极限抗拔力和有效锚固长度的研究
0 引言
随着城市空间的进一步扩大, 地下空间也得到了快速发展, 在沿海地区, 由于地下水位较高
近年来, 国内外关于锚杆的经济技术可行性、承载特性、粘结性能和破坏机理等方面的研究成果已取得较大进展
1 工程概况
辽宁省阜新玉龙时代广场地块北临龙湖路。场地地层为第四纪地层, 从上到下依次为杂填土、粉土含细砂、中粗砂、砾砂、中粗砂、强风化砂页岩、中风化砂页岩。试验锚杆全位于中风化砂页岩, 中风化砂页岩弹性模量为4.0GPa, 厚度为0.3~10.4m, 岩石饱和单轴抗压强度为40MPa, 主要为构造节理, 节理呈微张面, 贯通性好, 岩体完整程度低。
2 锚杆抗拔试验
本次试验采用在6根28mmⅢ级螺旋状冷拉钢筋抗浮锚杆表面粘贴应变片和全螺纹分布式裸光纤传感器的方式
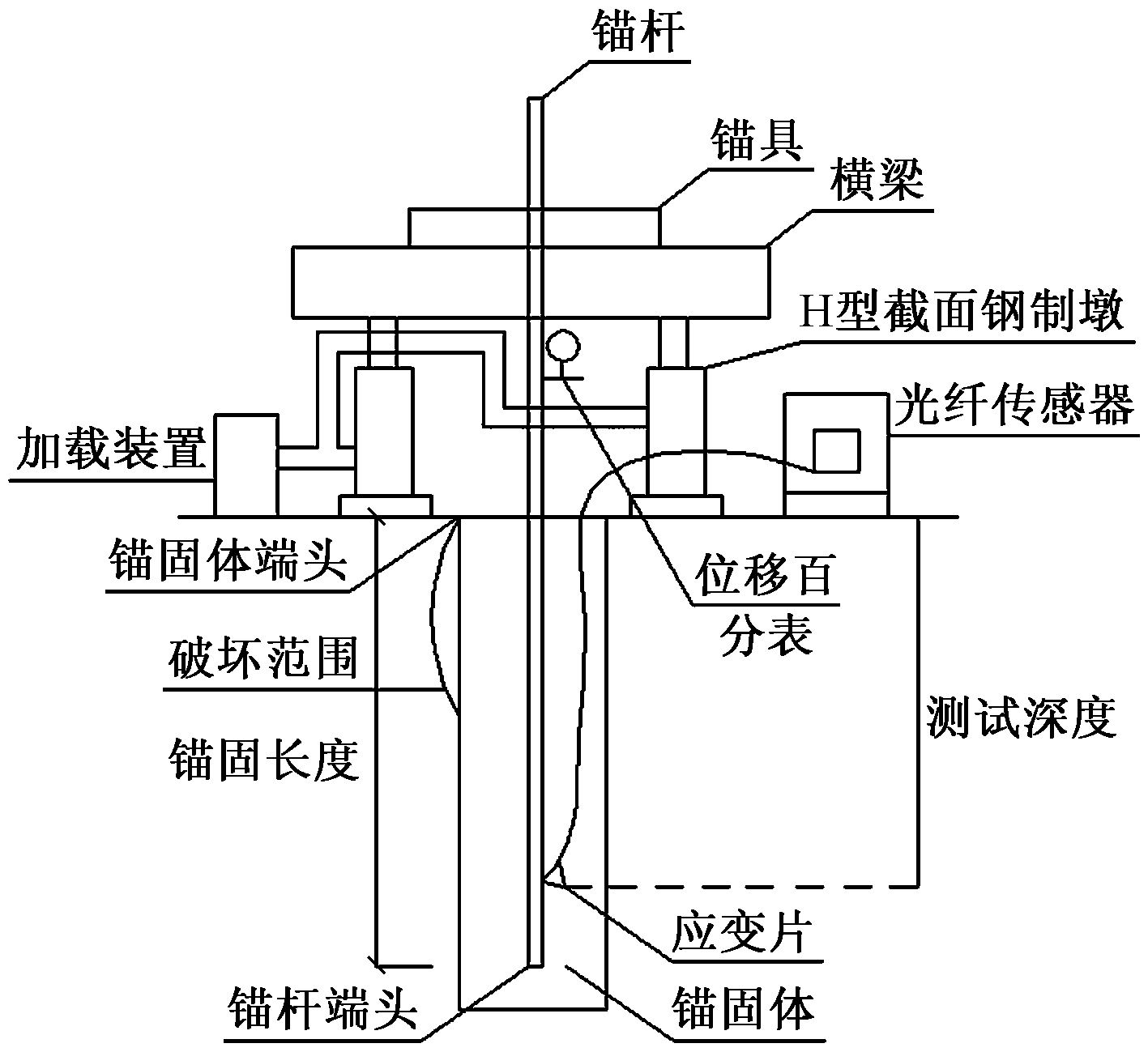
图1 锚杆试验装置图
3 试验结果及分析
3.1 锚杆破坏状态及荷载-位移曲线
1#~6#锚杆均出现锚头向上移动, 锚固体端部破坏的情况, 锚固体端部破坏范围是指从锚固体与锚杆的接触部位开始到锚固体裂纹消失为止处的垂直深度 (图1) , 1#~6#锚杆破坏时的最大加载荷载均为350kN。1#~6#锚杆的荷载-位移曲线见图3。

图2 试验现场
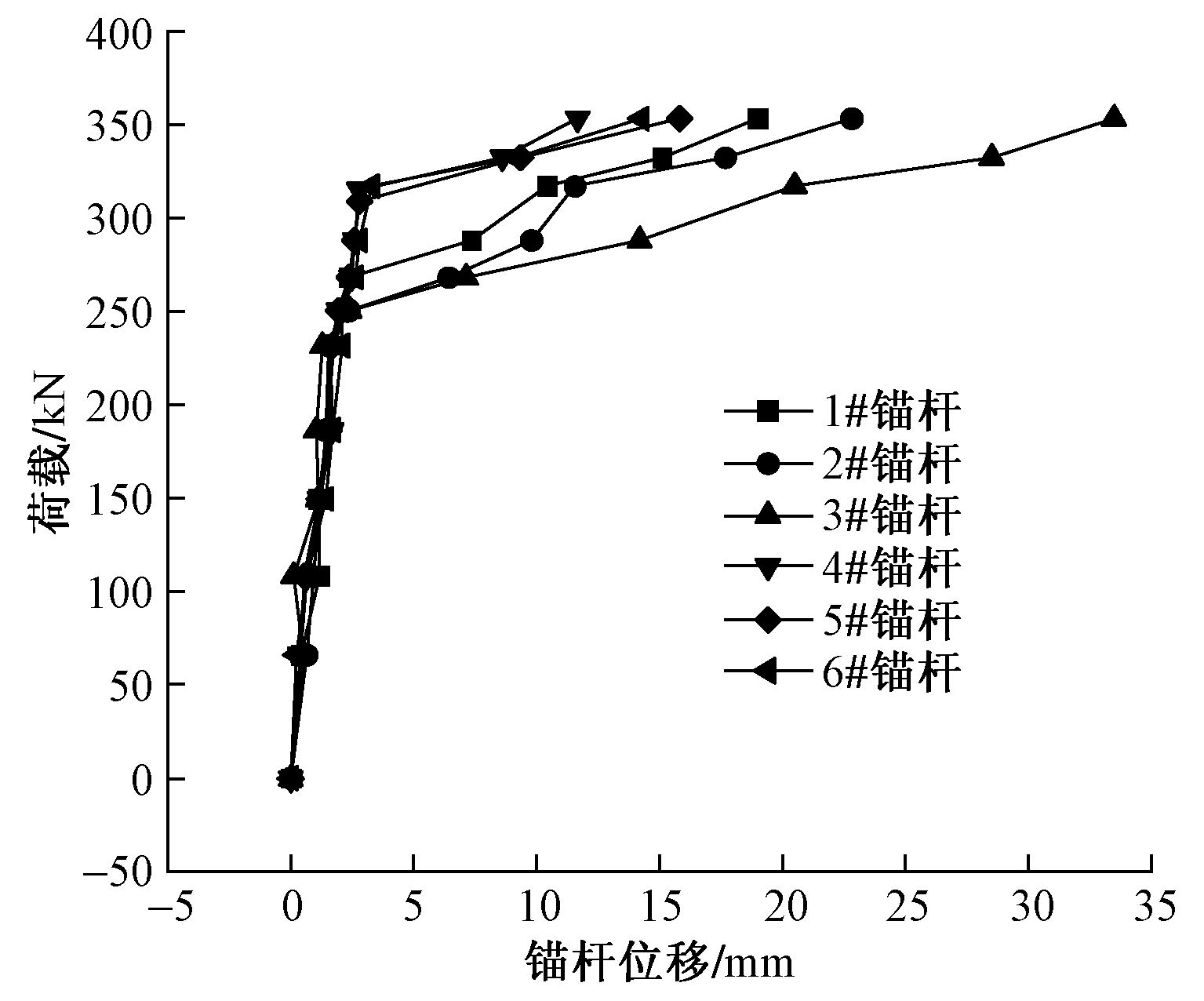
图3 1#~6#锚杆的荷载-位移曲线
从图3可以看出, 锚杆的位移随着荷载的增加而增加。当荷载较小时, 锚杆的荷载-位移曲线总体上呈线性变化, 当荷载逐渐增大时, 锚杆的荷载-位移曲线呈非线性变化, 且表现出荷载越大锚杆的位移增长速率也越大的规律。宋二祥等
表1 抗浮锚杆极限抗拔力及最大位移
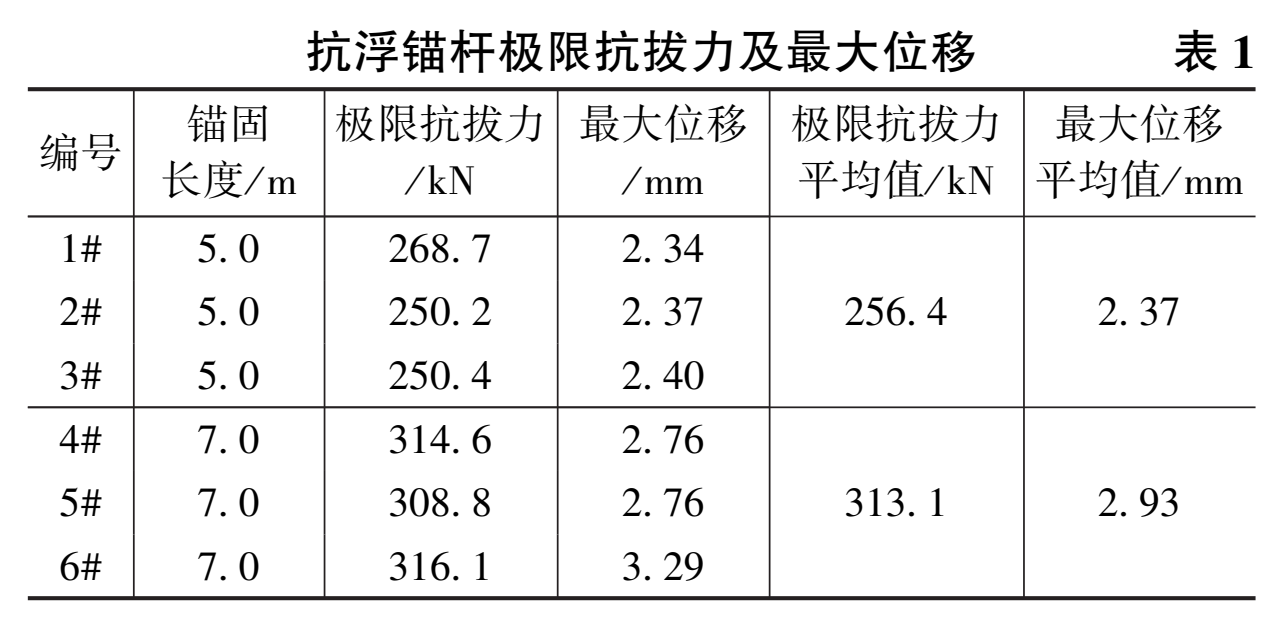
由表1可见, 1#~3#锚杆极限抗拔力平均值为256.4kN, 最大位移平均值为2.37mm;从图3可看出, 1#~3#锚杆在荷载250kN以下时, 其荷载-位移曲线呈线性, 3根锚杆荷载-位移曲线表现出十分相近的斜率, 此阶段抗浮锚杆处于弹性受力范围;在荷载250~268kN阶段时, 锚杆位移增长速率慢慢增大, 锚杆开始进入塑性变形阶段, 由于各锚杆极限抗拔力均位于250~268kN阶段内, 故锚杆在荷载250~268kN阶段的荷载-位移曲线相对荷载250kN以下的荷载-位移曲线有显著转折和波动, 表明此阶段锚杆逐渐进入塑性变形阶段;当荷载大于270kN时, 锚杆位移有显著增大, 表明锚杆完全进入塑性变形阶段。4#~6#锚杆极限抗拔力平均值达到313.1kN, 最大位移平均值为2.93mm, 锚杆在荷载308kN以下、荷载308~316k N阶段及荷载316kN以上这3个阶段的位移随荷载变化规律与1#~3#锚杆的规律相同。在同一地层结构条件下, 通过对比1#~3#锚杆与4#~6#锚杆的极限抗拔力平均值可知, 抗浮锚杆锚固长度增加可以显著提高锚杆极限抗拔力, 但随着锚杆锚固长度增加, 最大位移增加不显著, 即锚固长度与锚杆的极限抗拔力有关, 锚固长度越长, 极限抗拔力越大, 而锚固长度与锚杆的最大位移基本无关。
3.2 锚杆轴力分布
在感应系统中读出处于不同测试深度位置处的应变片数值, 即得出锚杆不同测试深度的应变值ε (每施加同一级别荷载时分别取5个不同测试深度的应变值) , 进而由下式推出锚杆在不同测试深度的轴力:
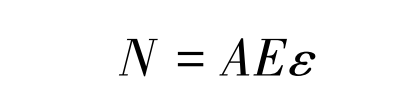
式中:A为锚杆杆体横截面面积;E为锚杆钢筋弹性模量。
不同荷载下, 6根锚杆轴力与不同测试深度的关系曲线见图4。从图4可看出, 1#~6#锚杆轴力分布基本相同, 随锚杆测试深度的增加, 锚杆轴力逐渐减小。从图4 (a) ~ (c) 可看出, 1#~3#锚杆在荷载低于270kN时, 锚杆轴力大体分布于测试深度3.6m以内;当荷载超过270kN时, 锚杆轴力随着荷载逐渐增大逐步向下移动。综上可知, 在荷载低于270kN时, 锚杆轴力主要在测试深度3.6m以内分布, 并随荷载增大而增大, 而在测试深度3.6m以下深度范围内增大幅度相对较小;当荷载大于270kN时, 在测试深度3.6m范围内, 轴力随荷载增大而增大的速度比在测试深度3.6m以下深度范围内的相应速度明显减小, 且在测试深度3.6m以下范围, 轴力的增大速率越来越大, 说明锚杆受拉时轴力不是均匀分布, 而是随荷载增大逐渐向下移动。从图4 (d) ~ (f) 中也可得出与4图 (a) ~ (c) 相同规律。原因如下:在给锚杆施加荷载时, 首先由杆体上部受力, 杆体上部变形较大导致其与砂浆的粘结力破坏而失效, 使得荷载沿杆体向下移动, 而270kN可近似视为锚杆与砂浆的粘结破坏强度。从图4可看出, 在达到锚杆与砂浆的粘结破坏强度之前, 随着荷载逐步增大, 锚杆轴力逐步向下移动, 锚杆锚固长度越大, 锚杆轴力向下移动的速率越大, 相反锚杆锚固长度越短, 锚杆轴力向下移动的速率越小。对比图4 (a) ~ (c) 和图4 (d) ~ (f) 可见, 1#~3#锚杆与4#~6#锚杆的杆体与砂浆的粘结破坏强度并没有太大变化, 均维持在270kN左右, 说明锚杆锚固长度对粘结破坏强度没有太大影响, 只能影响锚杆轴力的移动速率。
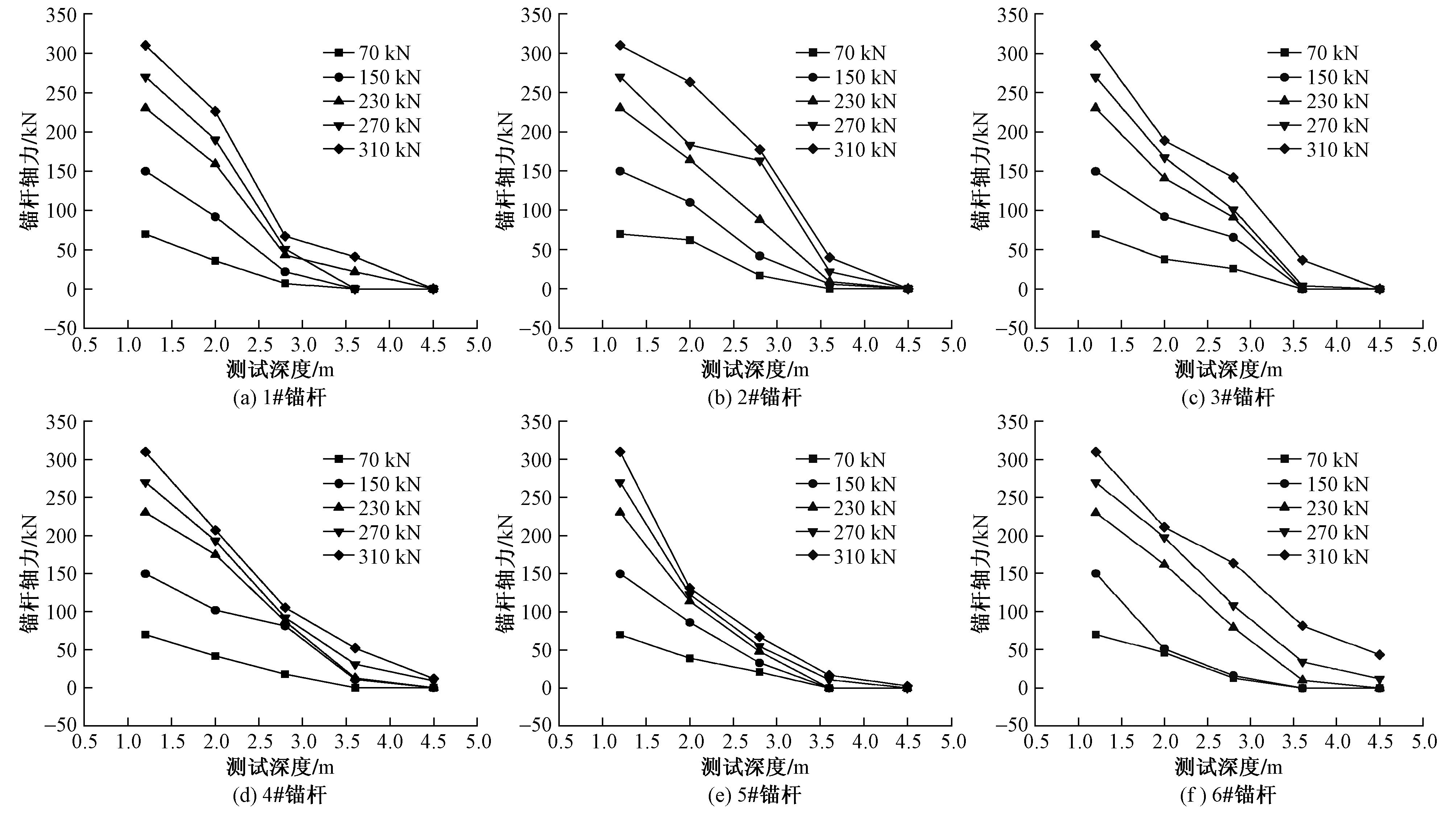
图4 1#~6#锚杆轴力随测试深度的变化
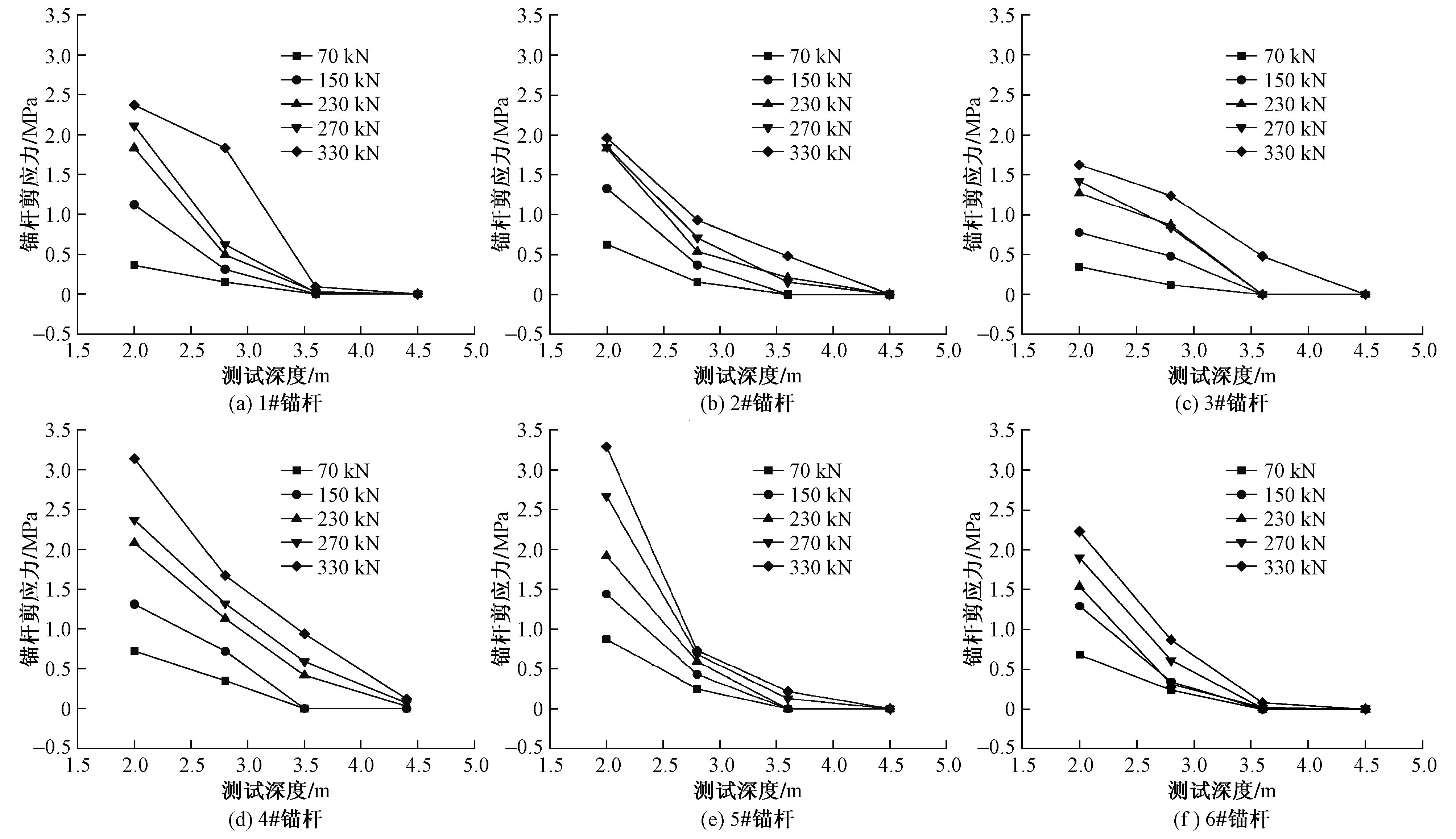
图5 1#~6#锚杆剪应力随测试深度的变化
3.3 锚杆剪应力分布规律
在外部荷载作用下, 相邻两根锚杆与锚固体之间的剪应力可由相邻两根锚杆的轴向拉力之差推算出, 锚杆第i点剪应力τi的计算公式[14]为:
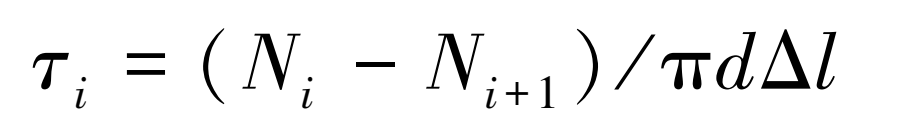
式中:Ni, Ni+1分别为锚杆在第i, i+1点的轴力;d为锚杆直径;Δl为两个锚点之间的水平距离。
6根锚杆的剪应力与测试深度的关系曲线如图5所示。试验分析表明, 6根锚杆的剪应力分布同样不均匀, 随着荷载逐渐增大, 剪应力的分布逐渐向下移动, 当荷载较小时, 剪应力大都分布于锚杆上半部分。从图5 (a) ~ (c) 可看出, 当锚杆在弹性范围内 (荷载330kN以下) 时, 随着荷载的增大, 剪应力只在测试深度3.6m范围内增大;当荷载达到330kN时, 剪应力开始传至测试深度3.6m以下, 此时杆体与锚固体的粘结力开始发挥作用。从图5 (d) ~ (f) 可看出, 当锚杆在弹性范围内 (荷载270kN以下) 时, 随着荷载的增大, 剪应力只在测试深度3.6m范围内增大;当荷载达到270kN时, 剪应力开始移动至测试深度3.6m以下, 此时杆体与锚固体的粘结力开始发挥作用。这进一步说明, 锚杆锚固长度确实对极限抗拔力有一定影响。
综上所述, 仅仅靠增加锚杆锚固长度来提高抗浮效果不是最有效的方法, 较大的位移也会导致锚杆稳定性降低, 使得锚杆的单位锚固力下降。此项目中, 中风化砂页岩中抗浮锚杆极限抗拔力取270~330kN, 有效锚固长度约3.6m, 建议实际锚固长度取为4.5m, 锚杆可使用的有效长度约4.5~5.0m。
4结论
(1) 锚杆的锚固长度与锚杆极限抗拔力有关, 锚固长度越长极限抗拔力越大;而锚固长度与锚杆的最大位移基本无关。
(2) 锚杆受拉时轴力不是均匀分布, 而是随荷载的增大逐渐向下移动。锚杆锚固长度越大, 锚杆轴力向下移动的速率越大, 锚杆锚固长度越短, 锚杆轴力向下移动的速率越小。
(3) 锚杆的剪应力分布同样不均匀, 随着荷载逐渐增大, 剪应力的分布逐渐向下移动, 当荷载较小时, 剪应力大都分布于锚杆上半部分。
(4) 锚杆的有效锚固长度与锚杆的锚固长度并无太大关系, 盲目增加锚杆锚固长度并不能无限提高抗浮效果。
(5) 本工程中风化砂页岩中的抗浮锚杆的极限抗拔力为270~330kN, 锚杆的有效锚固长度约为3.6m, 建议实际锚固长度取4.5m。
[2]白晓宇, 张明义, 闫楠.两种不同材质抗浮锚杆锚杆性能的现场对比试验研究与机理分析[J].土木工程学报, 2015, 48 (2) :38-58, 59.
[3]付文光.国内外锚杆试验类型简介[J].岩土工程学报, 2014, 36 (2) :191-197.
[4]张明义, 张健, 刘俊伟, 等.中风化花岗岩中抗浮锚杆的试验研究[J].岩石力学与工程学报, 2008, 27 (增1) :2741-2746.
[5]窦燕玲, 马国栋, 刘晓英.抗浮锚杆在高层结构地下车库工程中的应用[J].施工技术, 2016, 45 (1) :109-111.
[6]刘颖浩, 袁勇.全螺纹GFRP黏结型锚杆锚固性能试验研究[J].岩石力学与工程学报, 2010, 29 (2) :394-400.
[7]何思明, 李新坡.预应力锚杆作用机制研究[J].岩石力学与工程学报, 2006, 25 (9) :1876-1880.
[8]孙绍东, 胡海涛, 井彦青.抗浮锚杆合理设计探讨[J].建筑结构, 2013, 43 (22) :80-86.
[9]贾金青, 宋二祥.滨海大型地下工程抗浮锚杆的设计与试验研究[J].岩土工程学报, 2002, 24 (6) :769-771.