带托板无梁楼盖结构设计探讨
0 引言
无梁楼盖是一种很好的结构形式, 传力直接, 施工方便, 形式美观, 能有效降低层高, 充分发挥厚板的承载能力, 美国早在1906年就开始在实际工程中应用, 目前越来越多地用于地下室。以前由于有限元计算软件未普及, 设计师普遍采用经验公式进行计算, 存在较多局限性, 影响了无梁楼盖技术的发展。规范对无梁楼盖的设计也未有详细的说明, 在实际设计中存在一些争议或疑问。笔者将结合以往的工程经验, 根据一些算例, 对带托板的无梁楼盖设计经常遇到的几个问题进行探讨。
1 无梁楼盖的计算方法
无梁楼盖主要采用经验系数法
经验系数法、等代框架法都有其局限性, 在实际工程中往往难以完全满足其应用条件, 且为经验算法, 存在一定偏差
2 托板尺寸对无梁楼盖弯矩的影响
托板的尺寸指托板的平面尺寸和竖向厚度, 托板的尺寸主要由区格跨度和荷载大小决定。区格跨度大、荷载大, 托板的平面尺寸和竖向厚度也越大。若托板尺寸过小, 会导致冲切破坏, 或者用钢量过大。为了研究托板的合理尺寸, 笔者对不同荷载水平下不同托板尺寸对板带弯矩的影响做了分析, 下面以某一典型的地下车库为例进行讨论。该地下车库两层, 结构平面布置见图1, 无梁楼盖的柱帽采用平托板形式, 托板大样见图2, 混凝土强度等级为C35, 钢筋强度等级为HRB400, 均布活载为4kN/m2, 框架柱尺寸为600mm×600mm, 板厚为250mm。
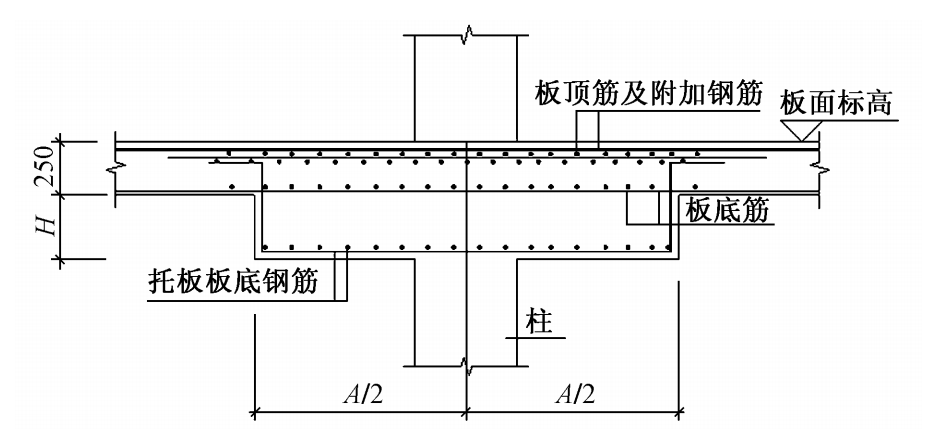
图2 托板大样
2.1托板平面尺寸对无梁楼盖弯矩的影响
托板厚度H取250mm, 托板平面尺寸分别取1.2m×1.2m, 1.8m×1.8m, 2.4m×2.4m, 3.0m×3.0m, 3.6m×3.6m, 采用MIDAS/Gen软件计算, 得到恒载 (自重) 与活载共同作用下各板带的弹性弯矩见表1, 仅活载作用下各板带的弹性弯矩见表2, 柱上板带支座弯矩及跨中弯矩与托板平面尺寸的关系曲线见图3。
托板平面尺寸与柱上板带弯矩 (恒载+活载) 关系表1
|
托板平面 尺寸/m |
Mxx1 / (kN·m) |
Mxx2 / (kN·m) |
Myy1 / (kN·m) |
Myy2 / (kN·m) |
| 1.2×1.2 | 1 121.4 | 348.8 | 855.6 | 337.4 |
| 1.8×1.8 | 1 266.8 | 308.8 | 966.6 | 290.2 |
| 2.4×2.4 | 1 407.1 | 269.7 | 1 046.6 | 246.6 |
| 3.0×3.0 | 1 540.2 | 238.8 | 1 133.8 | 212.4 |
| 3.6×3.6 | 1 655.3 | 203.1 | 1 228.2 | 189.8 |
由表1, 2及图3可以看出, 托板平面尺寸越大, 柱上板带支座处的弯矩越大, 跨中的弯矩越小。柱上板带的弯矩由两部分组成, 一部分由自重作用产生, 另一部分由活载产生, 经分解后发现, 随平托板尺寸增大, 由自重引起的柱上板带支座弯矩基本线性增加, 由自重引起的柱上板带跨中弯矩非线性减小, 而由活载引起的柱上板带支座弯矩非线性增加, 由活载引起的柱上板带跨中弯矩非线性减小。当托板平面尺寸增大到某个值后, 增加托板平面尺寸对减小柱上板带跨中弯矩不明显, 反而会由于自重的增加导致柱上板带支座弯矩不断增加。
托板平面尺寸与柱上板带弯矩 (活载) 关系表2
|
托板平面 尺寸/m |
Mxx1 / (kN·m) |
Mxx2 / (kN·m) |
Myy1 / (kN·m) |
Myy2 / (kN·m) |
| 1.2×1.2 | 431.2 | 135.7 | 307.0 | 131.5 |
| 1.8×1.8 | 489.1 | 120.4 | 362.4 | 112.6 |
| 2.4×2.4 | 536.5 | 104.9 | 396.0 | 96.0 |
| 3.0×3.0 | 575.5 | 91.0 | 417.2 | 82.1 |
| 3.6×3.6 | 596.2 | 78.2 | 433.2 | 72.0 |
2.2托板厚度对无梁楼盖弯矩的影响
取托板平面尺寸为1.8m×1.8m, 托板厚度H分别取150, 200, 250, 300, 350, 400mm, 采用MIDAS/Gen软件计算, 各板带的弹性弯矩见表3, 关系曲线见图4。可以看出, 随托板厚度增加, 板带支座弯矩增加, 跨中弯矩减小, 但托板厚度对弯矩的影响没有其平面尺寸对弯矩的影响那么明显。
托板厚度与柱上板带弯矩关系表3
|
托板厚度 /mm |
Mxx1 / (kN·m) |
Mxx2 / (kN·m) |
Myy1 / (kN·m) |
Myy2 / (kN·m) |
| 150 | 1 188.4 | 328.9 | 940.1 | 318.2 |
| 200 | 1 232.7 | 317.3 | 955.2 | 301.4 |
| 250 | 1 266.8 | 308.8 | 966.6 | 290.2 |
| 300 | 1 293.8 | 301.3 | 975.4 | 281.2 |
| 350 | 1 315.6 | 297.1 | 982.6 | 274.6 |
| 400 | 1 333.6 | 293.7 | 988.8 | 270.2 |
3 桩对无梁底板的影响
一般地下室的底板比较厚, 承台尺寸也比较大, 可以作为无梁底板的托板, 所以越来越多的地下室底板采用无梁楼盖结构, 不设基础梁, 这样既能有效发挥承台和底板的承载力, 又方便施工。承台一般上有框架柱, 下有桩, 若是单桩承台, 桩中心与框架柱中心一致, 与普通无梁楼盖受力模型一致, 但若是多桩承台, 桩与柱位置是错开的, 桩对承台有约束, 就会多处产生集中反力, 与普通的无梁楼盖有些不一样。笔者对是否考虑桩对承台的作用进行了对比, 某一层地下室无梁底板的平面布置见图5, 承台大样见图6。
承台厚度按1m考虑, 即托板厚度H=0.4m, 采用MIDAS/Gen软件分析, X向板带弯矩云图见图7, X向板带弯矩与到柱中心距离之间的关系见图8。结合图7、图8可以看出, 对两桩承台, 考虑桩对托板 (即承台) 的作用, 两桩之间的柱上板带支座弯矩减小比较明显, 减小约30%, 柱上板带跨中弯矩略有减小, 减小约10%, 跨中板带支座弯矩减小约23%, 跨中板带跨中弯矩减小约10%。对于Y向的板带, 考虑桩的影响, 无论是柱上板带还是跨中板带, 板带的弯矩都有不同程度的减小, 为节省篇幅, 就不再给出Y向板带弯矩云图。值得注意的是, 从图7 (b) 可以发现, 桩附近外侧的托板 (即承台) 和底板的弯矩有不同程度的增加, 增幅约10%~15%, 这是由于桩的作用, 改变了底板反力的分布形式, 即部分连续反力变为了集中力, 局部1m宽的支座板带区域出现了板带负弯矩较大的情况。所以这个区域的配筋宜加强, 若直接套用经验系数法会存在安全隐患。
4 承台厚度对底板弯矩的影响
以600mm厚底板为例, 分别计算了承台厚度为1 000, 1 100, 1 200, 1 300, 1 400, 1 500mm (对应的托板厚度H为400, 500, 600, 700, 800, 900mm) 时各板带的弯矩, 见表4。柱上板带弯矩-承台厚度关系曲线见图9。
由表4及图9可以看出, 随着承台厚度的增加, 柱上板带支座弯矩增加, 跨中弯矩减小, 但对跨中弯矩的影响不明显, 这可能是因为桩本来对承台 (兼托板) 就有很强的约束, 增加承台的厚度对刚度影响不大。笔者认为, 承台满足桩对承台的冲剪弯的作用前提下, 当承台厚度大于2倍底板厚度后, 再增加承台厚度, 不太经济, 因为此时支座弯矩增大主要是由于自重增加引起的。
承台厚度与柱上板带弯矩关系表4
|
承台厚度 /mm |
Mxx1 / (kN·m) |
Mxx2 / (kN·m) |
Myy1 / (kN·m) |
Myy2 / (kN·m) |
| 1 000 | 3 862.1 | 1 114.6 | 3 370.1 | 696.8 |
| 1 100 | 4 124.2 | 1 062.1 | 3 485.1 | 652.5 |
| 1 200 | 4 358.8 | 1 020.5 | 3 575.9 | 619.8 |
| 1 300 | 4 543.5 | 986.9 | 3 647.3 | 595.7 |
| 1 400 | 4 694.8 | 959.8 | 3 704.6 | 577.2 |
| 1 500 | 4 819.2 | 938.1 | 3 750.6 | 563.2 |
5 承台 (兼托板) 的配筋
有人认为, 多桩承台 (兼托板) 的配筋只要按承台计算就可以满足其作为无梁楼盖的托板的工况, 笔者认为要分情况考虑, 下面以两桩承台为例进行研究。
对于无筏板仅设拉梁的两桩承台, 承台配筋通常按跨中作用一个集中荷载的简支梁模型计算, 见图10。对设有筏板且承台间设基础梁的两桩承台, 考虑到水浮力和筏板自重先传递给基础梁, 然后由基础梁直接传给桩基或柱, 承台配筋也通常简化为前文无筏板的两桩承台, 按跨中作用集中荷载的简支梁计算。但对于无梁楼盖的筏板基础, 因没有基础梁, 筏板上的水浮力和筏板自重产生的内力会直接传递给承台 (兼托板) , 不能简化为图10简支梁的模型, 而应按图11所示的类似于连续梁的模型考虑水浮力和筏板自重对承台的影响。对某两层地下室的两桩承台进行分析, 其平面布置见图5, 仅考虑柱底内力对承台的作用, 按简支梁模型计算, 承台跨中弯矩为1 497.7kN·m, 考虑柱底内力、水浮力 (90kN/m2, 向上) 、筏板自重 (15kN/m2, 向下) 同时作用, 按图11所示的模型计算, 承台跨中弯矩为3 801kN·m, 说明若水浮力大于筏板自重, 对于无梁楼盖的筏板基础, 仅按图10所示的模型计算承台底部配筋是有严重安全隐患的;若水浮力小于筏板自重, 按图10所示的模型计算, 承台底部配筋能够满足柱底内力与桩反力共同作用下的承载力要求, 但由于筏板自重的作用, 承台作为无梁楼盖的托板, 其顶部钢筋有可能会不够。
所以对于无梁楼盖底板, 承台仅考虑传递上部荷载给桩基是不够的, 还应该考虑其作为无梁楼盖的托板传递筏板上的荷载给桩基, 按普通承台的配筋不能包络其既作为承台又作为无梁楼盖托板组合工况下的配筋, 对无梁楼盖底板的承台, 应同时考虑筏板、上部结构和桩基的影响, 进行整体分析。而且既要进行低水位或无水浮力工况下的分析, 也要进行高水位或抗浮水位工况下的分析, 进行包络设计。
6 托板最小配筋率
关于板柱结构, 2015年版《混凝土结构设计规范》 (
笔者认为对于普通的板柱结构, 一般托板的厚度由冲切控制, 而不是由受弯控制, 托板顶部的纵向受拉钢筋的最小配筋率可按混凝土规范8.5.3条执行, 但不宜小于0.15%, 若托板很薄, 应复核托板的受弯承载力。对于采用承台 (兼托板) 的地下室无梁底板, 单桩承台 (兼托板) 的配筋是由其作为托板的作用工况控制的, 其最小配筋率宜按混凝土规范执行, 但不宜小于0.15%;其他类型的承台 (兼托板) 的配筋是由其作为承台和托板组合工况共同控制的, 最小配筋率应同时执行混凝土规范和桩基规范的规定, 从严控制, 最小配筋率不宜小于0.15%和45ft/fy中的较大值。
7 经济性控制
无梁楼盖的板厚和用钢量主要取决于柱网尺寸和荷载大小及托板尺寸, 它们之间的关系的大致如下:设某板带弯矩Mi=Ki′qL2, 则该板带配筋ASi≈Mi/0.95hfy=Ki′qL2/0.95hfy, 若通长配筋, 则该板带用钢量为γ钢LASi, 假设X向跨度与Y向跨度相等, 均为L, 均摊到整跨框架内每平方米的用钢量si=γ钢LASi/L2≈KiqL/h, 各板带用钢量相加得s≈kqL/h。其中Ki′为板带弯矩影响系数;Ki为板带配筋量影响系数;γ钢为钢材容重, kN/m3;q为板上的均布荷载 (自重+附加恒载+活载) 设计值, kN/m2;L为柱跨, m;h为无梁楼盖的板厚, m;fy为钢筋抗拉强度设计值, kN/m2;s为楼盖每平方米的用钢量, kg/m2;k为与托板尺寸有关的系数。可以看出, 在两方向跨度相差不大的情况下, 每平米用钢量基本与荷载、跨度成正比, 与板厚成反比。通常板厚一般取短跨跨度的1/30~1/35
要注意, 采用有限元法计算出来的弯矩均是弹性弯矩, 实际上无梁楼盖是带裂缝工作的, 对无梁楼盖的板带进行配筋时, 首先要对弹性弯矩进行调幅, 笔者认为可以按梁的调幅系数0.85考虑。另外在实际配筋时, 柱上板带上部配筋宜采用拉通钢筋加支座附加钢筋的做法, 板带底部配筋若较多, 在满足计算和构造要求的前提下, 底部钢筋也可以部分不伸进支座, 锚入托板即可, 做到经济合理。
8 结论
(1) 无梁楼盖的板厚和托板尺寸的选择对经济性影响较大, 板厚宜取短跨跨度的1/30~1/35, 托板的厚度宜取板厚的 (1.0~1.2) 倍, 托板平面尺寸取柱宽加 (4~6) 倍板厚, 荷载大时取大值。
(2) 在两方向跨度相差不大的情况下, 无梁楼盖每平米用钢量基本与荷载、跨度成正比, 与板厚成反比, 即s=kqL/h。在荷载和板跨已经确定的情况下, 板厚和托板尺寸的选择对混凝土用量和钢筋用量影响较大, 另外配筋方式也会影响实际用钢量。
(3) 对采用承台 (兼托板) 的地下室无梁底板, 应考虑桩对托板的作用, 这样与实际受力情况一致。 若忽略桩的作用, 按普通无梁楼盖设计, 桩附近外侧的托板或底板会存在安全隐患。
(4) 对于兼托板用的多桩承台, 仅用单桩反力计算承台配筋是不正确的, 应该整体建模, 同时考虑上部墙柱、下部桩基、水浮力和筏板自重的作用, 整体分析计算, 并宜进行最低水位和最高水位两种工况的包络设计。
(5) 采用有限元算法, 宜对弯矩进行调幅, 利用调整后的弯矩对各板带进行配筋设计, 不能盲目套用软件的配筋结果。
(6) 规范虽然只要求验算柱帽的冲切, 笔者认为若采用有限元计算, 对于带托板的无梁楼盖还需
验算托板的受弯承载力, 在满足受弯承载力的前提下, 最小配筋率可适当减小。
[2]逯晔, 徐晶.地下车库无梁楼盖设计常见问题讨论[J].建筑结构, 2015, 45 (4) :60-63.
[3]混凝土结构设计规范:GB 50010—2010[S].2015年版.北京:中国建筑工业出版社, 2015.
[4]建筑桩基技术规范:JGJ 94—2008 [S].北京:中国建筑工业出版社, 2008.
[5]朱聘儒.双向板无梁楼盖[M].北京:中国建筑工业出版社, 1999.









