随着我国经济和文体事业的快速发展, 大跨度屋盖结构蓬勃兴起, 广泛应用于机场、体育馆、会展中心、文化广场、火车站等大型重要公共建筑中。这类结构集合了新材料、新技术的应用, 具有自重轻、柔度大、阻尼小等特点, 风荷载往往成为其主要控制荷载。

　　 建筑的门窗被强风吹开或受损等突变事故的发生可能会在建筑物上形成开孔, 导致风从孔洞突然涌入建筑物, 室内脉动内压急剧变化, 从而使屋盖结构受内外压共同作用而遭受风致破坏。此外, 当施工期间围护结构尚未全部完成时, 建筑物处于局部敞开的状态, 屋盖结构也会受到内外压的共同作用而处于比正常使用阶段更不利的状态。屋盖结构受内外压共同作用而导致破坏的实例时有报道, 1992年美国佛罗里达地区的Andrew飓风期间, 出现因受内外压共同作用而致使屋面破坏的情形;1996年南印度洋飓风期间, 印度沿海受影响地区的很多房屋因通风装置和窗户的破坏使飓风从孔洞涌入建筑内部, 内压的急剧增大使山墙倒塌和屋面破坏;1996年9月, 在台风莎莉 (Sally) 的影响下, 湛江市体育中心体育馆迎风面的幕墙破坏达到85%, 而背风面的幕墙在迎风面幕墙损坏后, 风进入馆内而受到贯穿破坏, 同时进入馆内的风将轻型屋盖面板掀掉, 造成较大的经济损失;2010年9月第10号台风“莫兰蒂”造成泉州海峡体育中心体育馆多处脱落长达10多米的屋面板, 同时由于风从孔洞涌入馆内, 使馆内设施及幕墙遭到不同程度的破坏;2010年12月10日, 因遭遇10级强风, 北京首都机场T3航站楼屋顶两处金属屋面板被掀开, 破损面积约200m², 造成较大的经济损失;2011年4月22日, 美国圣路易斯市的兰伯特-圣路易斯国际机场遭到龙卷风袭击, 机场建筑严重受损, 迎风面玻璃幕墙破碎, 导致风从孔洞涌入造成多人受伤, 导致机场关闭, 灾后调查表明, 迎风面幕墙突然破坏引起的内部风效应是导致结构破坏的重要原因。综上所述, 在重要建筑的抗风设计中, 有必要考虑幕墙开孔洞状态下的风荷载特性, 这也是结构风工程领域的一个重要研究方向。

　　 Holmes^[1]首先采用了声学中空腔的Helmholtz共振原理来研究内压共振效应;Liu等^[2]研究了开孔大小和开孔位置对内压响应共振振幅的影响;Stathopoulos等^[3]对开孔结构的内压瞬时响应进行了风洞试验和理论研究, 发现内压系数瞬时响应的极值随迎风面开孔尺寸的增大而增大;Sharma等^[4]对单一主洞口下围护结构柔度对风致内压和净风压的影响进行了研究, 认为柔性屋面在Helmholtz频率处的紊态能量约为相同尺寸的刚性屋面的25倍;Yu等^[5]对开孔后的大跨屋盖结构风致振动及风致内压进行了研究, 对内压理论计算的相关参数进行了修正。

　　 目前国内外荷载规范^[6,7,8,9,10]对建筑内部风压系数的规定各有差异。

　　 中国内地荷载规范^[6]分别对封闭式建筑、仅一面墙有主导洞口的建筑的内部局部体型系数进行了规定, 但对非主导洞口的建筑物并未做相关说明;中国香港荷载规范^[7]仅对四周封闭建筑的内压系数进行了规定, 但对有幕墙开洞建筑, 其内压系数则需经风洞试验确定。

　　 日本荷载规范^[8]也对四周封闭建筑的内压系数进行了规定, 但对有幕墙开洞的建筑内压系数则需经风洞试验确定;美国荷载规范^[9]对四周封闭与幕墙开洞建筑的内压系数进行了规定, 但并未指出内压系数大小与开洞位置及来流风向之间的关系;相比之下, 澳洲规范^[10]对建筑内压系数的规定较为全面。

　　 上述规范规定值对体型复杂且幕墙开洞率不同的大跨屋盖结构是否适用, 仍有待进一步研究。

　　 本文利用刚性模型风洞试验, 研究大跨屋盖结构在迎风面幕墙突然开孔下屋盖风荷载的变化, 同时将不同开洞率下屋盖结构的风荷载特性与国内外规范值进行详细的对比分析, 提出可供结构设计及荷载规范修订的参考依据。

　　 本文研究的大跨屋盖结构的实际尺寸为162m×100m, 屋顶高55m, 矢跨比为0.015, 屋檐长向悬挑15m, 短向悬挑10m, 结构形式为四边支承的双层网架结构。风洞试验模型 (图1) 缩尺比为1∶300, 模型壁厚为10mm, 模型基本尺寸见表1, 模型测点分布洞口编号及风向角示意见图2。风洞试验是在湖南大学建筑安全与节能教育部重点实验室的建筑与环境风洞试验室进行的, 试验时扫描阀测压信号采样频率为500Hz, 采样时间为40s。风剖面及湍流度剖面按照中国内地荷载规范^[6]B类地貌进行模拟。试验中取参考点高度为0.2m, 参考点风速为10m/s。图3给出了风洞中0.2m高度处的顺风向脉动风谱, 可以看出, 风洞中的顺风向脉动风谱与常用的理论谱 (Karman谱、Kaimal谱、Davenport谱) 基本一致。

　　 为保证试验模型开洞位置在关闭状态下 (无孔洞时) 的密闭性, 特研发了一种风洞试验中测试建筑物内压的开启装置, 并申请了专利^[11], 采用此装置可有效保障试验模型内压测试的顺利进行。

　　 为了较为详尽地对比分析不同开洞率下屋盖风荷载特性的差异, 本试验对迎风面、背风面、侧风面不同开洞率进行了组合, 共计45个工况, 因篇幅有限, 选取其中具有代表性的12个工况进行分析研究, 试验工况见表2, 其中迎风面、背风面、侧风面均根据风向角为0°进行定义。

　　 关于紊流风场中开孔结构风致内压的理论研究, 自Holmes^[1]提出内压传递方程的基本形式后, 国内外学者对其进行了不断的完善, 但提法略有差异, 一般认为Sharma和Richards^[12]提出的三参数方程适用性较广, 即:

　　 式中:γ为比热比;ρ_α, p_α分别为大气密度和压强;A_o为开孔面积;c为开孔收缩系数;L_e为开孔处气流的有效长度;V_o为建筑内部容积;C_pi, C_pw分别为内部压力系数和孔口处的外部压力系数;q为参考点风压, 其中ρ_a为参考点处空气密度, U₁₀为参考风速。

　　 内 (外) 部风压系数可由下式计算:

　　 式中:c_pi (t) 为试验模型内 (外) 表面第i个测压点所在位置处的风压系数;p_i (t) 为所测得的模型内 (外) 表面第i个测压点所在位置处的风压;p₀为参考高度点处的平均总压;p_∞为参考高度点处的平均静压。

　　 对于开孔深度很小的建筑物, 可以不考虑孔口的气流有效长度其中C_I为孔口处惯性系数。根据声学关系式γp_α=ρ_αa_s², Helmholtz频率f_H可以表达为下式:

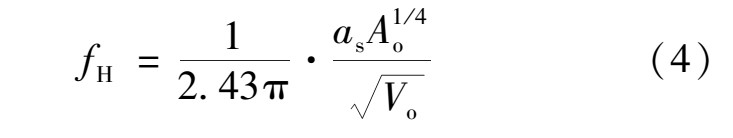
　　 式中a_s为空气中声音传播的速度。

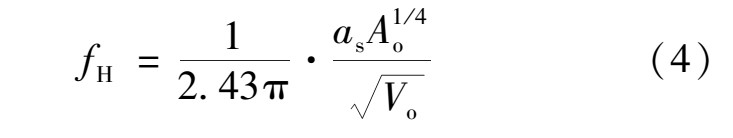
　　 在本文研究中, 因只涉及到一个试验模型, 故V_o为定值, 取a_s=340m/s, V_o=0.03m³, 文献[2-5]中开孔面积A_o一般指迎风面开孔面积, 故本文仍沿用此规定。显然, 按照迎风面开洞面积进行理论分析时, Helmholtz频率的大小与背风面及侧风面的开洞面积无关, 各工况下的Helmholtz频率理论计算值见表3。

　　 由于大型公共建筑在使用过程中部分门窗会突然打开, 同时也会出现幕墙在强风作用下突然破坏的现象, 因此对此类建筑有必要对其屋盖结构在幕墙突然破坏时的风荷载特性进行分析。图4为工况1典型内表面测点在突然开洞下的内压系数时程曲线, 从图中可以看出:1) 各测点在幕墙开洞前后内压系数时程曲线基本一致, 这是由于在给定的边界层空间中, 空气压力的传播速度为音速, 内部压力在瞬间达到均等, 因此可以用统一的内压系数时程来描述结构内压的特性。2) 在迎风面墙体突然开洞时, 内压系数从开洞前的0.3左右瞬间增大到0.8左右 (图4 (a) ) ;在背风面开洞后, 内压系数有所降低, 但降低幅度较为缓慢 (图4 (a) ) 。3) 当开洞位置处于侧风面时, 先开启一侧洞口的瞬间, 内压有微弱的减小, 但是瞬间便恢复到开洞前的内压值并达到相对平稳状态, 而再次开启对应侧洞口时, 内压变化并不明显 (图4 (b) ) , 由此可见, 当迎风面、背风面无孔洞, 侧风面开洞的先后顺序对建筑内压的影响较小。

　　 为了便于对试验结果进行对比分析, 根据所选取的试验工况研究, 对其进行了分类:第一类为仅开启横墙洞口, 但开启横墙的洞口顺序及开启的开洞率不同, 为工况1~3;第二类为开启横墙与一侧纵墙的洞口, 为工况4~7;第三类为先开启横墙洞口后, 再开启一侧或者两侧纵墙洞口, 为工况4和工况8;第四类为四面墙洞口均开启, 但各墙的开启开洞率及开启洞口顺序均有差异, 为工况9~12。其中第二类侧重于分析横墙、纵墙开洞率均不同的工况;第三类侧重于分析横墙开洞率不变而纵墙开洞率有差异的工况。此外, 为增强试验结果的可比性, 各工况均取横墙处于迎风面或背风面时的风向角数据, 即取0°或180°风向角数据进行对比分析研究。

　　 图5为不同工况下测点R13-D内压系数自功率谱, 从图中可以发现:1) 所选取的工况中, 在高频区存有较多的谱峰值, 最大的谱峰值 (共振频率) 均出现在30~40Hz之间, 这与第2节所述的Helmholtz频率理论计算值有一定的差别, 笔者认为引起此差异的主要原因是: (1) 本文模型的设计与文献[1-5], [12-16]中试验模型的设计不同; (2) 本文研究同时考虑了迎风面、背风面、侧风面墙体开洞率的影响, 而理论计算公式仅考虑了迎风面墙体的开洞率。2) 迎风面墙体开洞率越大, 内压脉动能量越大。3) 开洞瞬态的脉动能量在低频段衰减较为明显, 高频段的共振现象没有开洞稳定后显著。4) 当背风面墙体无开洞时, 内压系数低频段的能量随着侧风面开洞率的增加而减小, 内压脉动能量也随之有明显减小。5) 开洞数量对内压脉动的影响没有明显的规律可循, 即并不是开洞数量越多, 内压脉动就越剧烈, 这与文献[17]所论述的一致。

　　 为了更好地了解内部测点脉动风压功率谱的变化, 在0°, 180°风向角情况下, 选取测点R13-D为研究对象进行分析, 其脉动风压归一化功率谱如图6所示。从图中可以发现:1) 无论是开洞瞬态还是开洞稳定后, 各工况脉动风压归一化功率谱在高频段均出现明显的向上翘曲, 说明测点在各工况下的脉动风压归一化功率谱高频成分占有较大比例;2) 在折减频率为3附近时均出现明显的谱峰值, 但最大谱峰值均出现在高频段区域;3) 各工况下, 测点在开洞瞬态与开洞稳定后的脉动风压归一化功率谱的变化趋势较为接近, 说明幕墙开洞数量及开洞位置的变化对内压脉动能量的影响较小。

　　 本文所选工况的内压系数试验值与荷载规范^[6,7,8,9,10]的规定值对比见表4。从表中可以看出:1) 相同工况下, 各测点的内压系数差异较小, 因此可以采用其中某个测点的结果来代表模型内部测点的内压系数值;2) 当模型四周封闭时, 内压系数为0.34左右, 均大于列表中荷载规范^[6,7,8,9,10]规定值, 说明荷载规范^[6,7,8,9,10]对封闭建筑内压系数的规定值相对较小;3) 当迎风面开洞率为5%, 背风面开洞率为10%, 两侧风面开洞率各为4.2%时, 内压系数最小, 为0.39;当迎风面开洞率为10%, 侧风面开洞率为4.2%, 背风面无开洞时, 内压系数达到最大, 为0.75;4) 当幕墙有开洞时, 各工况下的内压系数均大于澳洲荷载规范^[10]的规定值;5) 对比美国荷载规范^[9]的规定值, 工况2, 4, 6, 7, 11的内压系数均大于此规范的规定值, 其他工况的内压系数均小于此规范的规定值或与规定值大小相当。综上所述, 考虑结构安全与经济因素, 在目前中国内地荷载规范^[6]对非主导洞口建筑物的内压系数规定较欠缺的情况下, 对开洞建筑的内压进行风洞试验评估是很有必要的。

　　 悬挑雨篷、开敞建筑的屋盖等结构一般根据测点的综合风压系数进行设计。本研究中, 当横墙垂直于来流风向时, 气流沿横向屋檐发生分离与再附, 屋盖上表面与横墙平行的测点风压系数较为均等, 而屋盖内部各测点在同一工况下风压系数基本相等, 故在屋盖迎风面、背风面及屋脊处各取1个测点, 共3个典型测点作为研究对象。用幕墙开洞时屋盖测点的综合风压系数与四周封闭时屋盖相应测点的综合风压系数比值的大小来衡量幕墙开洞后屋盖风压系数的变化。

　　 各工况下典型测点综合风压系数见表5, 从表中可以看出:1) 当幕墙有开洞时, 屋盖的综合风压系数得到了不同程度的放大;2) 各工况中屋脊处测点 (R13) 的综合风压系数放大率均小于迎风面屋面测点 (测点R8) 与背风面屋面测点 (R18) 的放大率;3) 当迎风面幕墙的开洞率为10%, 背风面幕墙无开洞, 一侧风面幕墙开洞率为4.2%时, 屋盖的综合风压系数放大率达到最大, 其中迎风面屋面的综合风压系数比值为1.41;4) 传统结构设计时, 仅考虑四周封闭时的屋盖风压系数, 但当有幕墙开洞时, 屋盖风压系数变化较大, 因此结构设计时应根据实际幕墙开洞情况对屋盖结构进行设计。

　　 本文通过对不同幕墙开洞率的大跨屋盖结构刚性模型风洞试验研究, 得出了以下结论:

　　 (1) 当迎风面幕墙有突然开洞发生时, 内压时程有明显的突变, 但开洞位置处于侧风向时, 变化较小。

　　 (2) 通过对测点的内压系数功率谱分析发现, 所选取的各工况中, 在高频区存在较多的谱峰值, 屋盖共振频率均出现在30~40Hz之间, 与理论计算方法得出的屋盖Helmholtz频率理论计算值有一定的差异, 笔者认为引起此差异的主要原因是:1) 本文模型的设计与文献中试验模型的设计有所不同;2) 本文研究中同时考虑了迎风面、背风面、侧风面墙体开洞率的影响, 而理论计算公式仅考虑了迎风面幕墙的开洞率。

　　 (3) 内压脉动能量随迎风面幕墙开洞率的增大而增大;突然开洞时瞬态内压的脉动能量在低频段衰减较为明显。

　　 (4) 对测点脉动内压归一化功率谱分析发现, 无论在开洞瞬态还是开洞稳定后, 各工况高频段均出现明显的向上翘曲, 高频成分占有较大的比比例。

　　 (5) 将内压系数试验值与国内外风荷载规范^[6,7,8,9,10]的规定值进行了详细的对比研究, 发现幕墙无孔洞时的内压系数均大于荷载规范^[6,7,8,9,10]的规定值;有幕墙开洞时的内压系数试验值均大于澳洲荷载规范^[10]的规定值;随着墙面开洞率的变化, 内压系数试验值与美国荷载规范^[9]的规定值差异较大。

　　 (6) 对幕墙有无开洞的屋盖综合风压系数进行了对比分析, 发现有幕墙开洞时, 屋盖综合风压系数明显增大, 结构设计时应根据实际幕墙开洞情况对屋盖结构进行抗风设计。

　　 本文所得结论对有幕墙开洞的大跨屋盖结构的抗风设计及中国内地荷载规范^[6]中关于非主导洞口建筑内压的修订均具有一定的参考借鉴意义。