新型闭口压型钢板组合楼板抗火性能影响因素研究
0 引言
近年来, 压型钢板组合楼板在房屋建筑中的应用逐渐增多, 已从开口压型钢板组合楼板发展到新型闭口压型钢板组合楼板。
国内外针对组合楼板的抗火性能已有较多研究, 但大多局限于开口压型钢板组合楼板。1989年, G M Newman
国内对火灾下组合楼板温度场也有较多研究, 2006年, 董建莉等
国内外相关设计方法主要针对开口压型钢板组合楼板, 难以直接应用于近年来应用日益增多的闭口压型钢板组合楼板。本文采用数值计算方法对闭口压型钢板组合楼板抗火性能进行参数化分析, 主要考虑了荷载水平、几何及材料属性等影响因素, 并提出该类组合楼板抗火性能计算方法建议。
1 数值计算模型
1.1 有限元模型
本文采用通用有限元计算软件ABAQUS建立组合楼板非线性有限元计算模型。为减少计算量, 建立组合楼板沿跨度方向一半的对称模型, 跨中约束转动分量, 端部采用简支边界条件, 混凝土采用实体单元, 压型钢板采用壳单元。
模型分析为模拟组合楼板火灾试验常采用的瞬态分析, 首先对模型进行热传导分析, 得到组合楼板在受火升温时间范围内的温度场变化。热传导分析中, 楼板顶面不受火面与空气之间采用对流换热边界条件, 对流换热系数为25W/ (m2·℃) ;假设楼板宽度方向两侧为绝热边界条件, 钢板底面直接受火, 受热对流和热辐射作用, 对流换热系数为25W/ (m2·℃) , 辐射换热系数为0.5。需要说明的是, 压型钢板的闭口部分由于几何形状的屏蔽作用, 不会直接受到热辐射影响, 同时难以直接接触热空气, 因此闭口部分不设置辐射换热边界条件, 对流换热系数取可忽视的较小值。
模型中混凝土和钢材热工参数值均采取随温度变化值, 混凝土本构模型采用塑性损伤模型, 受拉部分用应变能定义;压型钢板采用理想弹塑性模型, 材料热工参数及本构模型取值来源如表1所示。
有限元模型材料参数来源表1
|
混凝土材料参数 |
参考文献 | 压型钢板材料参数 | 参考文献 |
|
比热容 |
文献[8] | 比热容 | 文献[8] |
|
导热系数 |
文献[8] | 导热系数 | 文献[8] |
|
热膨胀系数 |
文献[9] | 热膨胀系数 | 文献[9] |
|
本构模型抗压段 |
文献[9] |
本构模型 (弹性模量 及屈服强度) |
文献[7] |
|
本构模型抗拉段 |
文献[10] |
在对楼板进行均布荷载作用下的力学分析中, 考虑混凝土和压型钢板的接触作用, 用ABAQUS中的Connector单元模拟其非线性接触关系。其剪切滑移曲线在常温下的取值参考王元清等
有限元分析模拟实际耐火试验中加载及受火升温过程, 采用两个分析步。第一个分析步中施加均布荷载, 第二个分析步中导入热分析中计算好的温度场数据进行耐火计算。组合楼板计算模型如图1所示。
1.2 模型验证
为验证有限元模型的有效性, 本文利用不同厚度闭口压型钢板组合楼板耐火试验结果进行分析验证。压型钢板为普通钢材, 采用Encondek 65-555型号, 钢材屈服强度为475MPa, 钢板厚度为1.0mm, 楼板宽度555mm;混凝土强度等级为C30。闭口压型钢板截面及试件截面几何参数见图2和表2。
试件截面几何参数/mm 表2
|
试件编号 |
压型钢板厚度 | 楼板厚度 | 净跨 | 总跨 |
|
E-115 |
1.0 | 115 | 3 290 | 3 600 |
|
E-125 |
1.0 | 125 | 3 290 | 3 600 |
|
E-150 |
1.0 | 150 | 3 290 | 3 600 |
|
E-180 |
1.0 | 180 | 3 290 | 3 600 |
组合楼板的抗火有限元计算与试验结果对比如表3所示。从表3可看到, 有限元计算结果和试验结果有较高的吻合度。楼板厚度在115, 125mm时首先达到绝热条件, 即背火面升温超过140℃;更厚的楼板则先达到变形条件限值, 因挠度过大而达到耐火极限。从绝热耐火时间来看, 115mm厚楼板及125mm厚楼板绝热耐火时间分别超过90min和120min, 更厚的楼板绝热耐火时间可达到或超过3h, 均满足民用建筑最高耐火极限的要求。
组合楼板抗火有限元计算与试验结果对比表3
|
试件编号 |
变形耐火时间/min |
绝热耐火时间/min | ||
|
有限元结果 |
试验结果 | 有限元结果 | 试验结果 | |
|
E-115 |
155 | >105 | 105 | 105 |
|
E-125 |
176 | >120 | 121 | 120 |
|
E-150 |
177 | 172 | 176 | >172 |
|
E-180 |
209 | >180 | 288 | >180 |
以试件E-115为例, 其楼板截面温度场变化情况及挠度发展的有限元计算结果与试验结果对比如图3, 4所示。有限元模型中, 楼板背火面温度测点以及压型钢板温度测点随时间变化规律均与试验结果有较好的吻合度, 挠度发展曲线与试验结果接近, 误差在10%以内。综上所述, 该有限元模型的有效性和准确性得到了验证, 可以用于后续进一步的参数分析。
2 组合楼板抗火性能影响因素
利用上述有限元分析模型, 对影响组合楼板抗火性能的主要参数进行分析计算, 对比分析了闭口压型钢板组合楼板及开口压型钢板组合楼板温度场的发展趋势;针对楼板变形耐火极限, 考虑了楼面荷载、混凝土及钢材材料强度、楼板及压型钢板厚度、钢材耐火性等因素的影响。每个影响参数取五个不同值, 各个参数变化如表4所示。
算例参数取值表4
|
压型钢板 厚度/mm |
组合楼板 厚度/mm |
混凝土 强度等级 |
钢材屈服 强度/MPa |
楼面均布荷载 / (kN/m2) |
|
0.5 |
115 | C20 | 250 | 4.5 |
|
0.75 |
125 | C25 | 320 | 6.0 |
|
1.0 |
135 | C30 | 350 | 7.5 |
|
1.25 |
150 | C35 | 475 | 9.0 |
|
1.5 |
180 | C40 | 550 | 10.5 |
2.1 截面温度场分布
通过试验及数值模拟可知, 压型钢板的顶部闭口翼缘部分温度发展较慢, 达到90min耐火时间时, 尽管压型钢板底部温度已经高达900℃, 但闭口部分温度仍不足600℃, 这个特性与开口压型钢板组合楼板有着显著不同。
图5对比了四种不同厚度开口压型钢板组合楼板和闭口压型钢板组合楼板的底面及顶部温度发展曲线。图中115开口底面表示115mm厚开口压型钢板组合楼板底面;E-115闭口底面表示115mm厚闭口压型钢板组合楼板底面, 余类同。从图5可以看到, 两种组合楼板的压型钢板的底面温度发展较为相似, 曲线有较高的重合度;但开口顶部和闭口顶部温度相差较大, 开口压型钢板顶部温度接近于闭口底面温度, 在90min时温度达到800℃;闭口压型钢板的闭口顶部温度发展较慢, 90min时不到600℃。这种温度分布的差异来自于两种组合楼板几何形状的不同带来的受火条件的变化:开口压型钢板组合楼板的压型钢板全部暴露在火灾条件中, 压型钢板所有部分均直接受到热对流和热辐射作用;闭口压型钢板组合楼板闭口部分由于混凝土屏蔽作用, 受到的热辐射作用几乎为零, 热对流的烟气也很难达到钢板的闭口部分。
图6为相同板厚的开口与闭口压型钢板组合楼板受火90min时的等温线, 从图6中可以明显看出, 开口压型钢板组合楼板 (图6 (a) ) 顶部直接受火, 整块组合楼板受火面积更大、上方混凝土楼板更薄;开口压型钢板组合楼板在同一时刻比闭口压型钢板组合楼板 (图6 (b) ) 温度更高, 且温度分布更不均匀。
综上所述, 相对于开口压型钢板组合楼板, 几何形状为闭口型的组合楼板提供了更好的隔热条件, 截面温度发展更慢。闭口压型钢板组合楼板具有更好的隔热性能和抗火性能。
2.2 压型钢板厚度
取0.5, 0.75, 1.0, 1.25, 1.5mm五个不同压型钢板厚度值进行计算分析。根据挠度达到规范要求限值确定其耐火时间, 并与蒋首超等
对于闭口压型钢板组合楼板, 钢板厚度从0.5mm增加到1.0mm时, 耐火时间约提高15%。钢板厚度越大, 抗火性能越好, 但增加趋势放缓, 在曲线族上表现为越往上曲线越密集。这种变化的原因是钢板厚度较大时, 压型钢板提供的承载作用出现富余, 组合楼板的承载能力主要由混凝土部分起控制作用, 因此钢板厚度的增加对于提高楼板抗火性能的作用越来越小。
2.3 压型钢板强度
取常规250, 320, 350, 475, 550MPa五个不同压型钢板屈服强度进行计算分析。根据挠度达到规范要求限值确定其耐火时间, 分析结果如图8所示。
由图8可知, 与压型钢板厚度对组合楼板抗火性能的影响一致, 钢板强度越大, 组合楼板抗火性能越好。当压型钢板屈服强度增加1倍时, 耐火时间提高40%左右。这同样归功于闭口压型钢板组合楼板中闭口部分温度上升慢, 该部分钢材仍可以在升温后期发挥承载作用。
2.4 楼板厚度
取115, 125, 135, 150, 180mm五个不同楼板厚度值进行计算分析。根据挠度达到规范要求限值确定其耐火时间, 并与蒋首超等
由图9可知, 显然, 楼板厚度对楼板抗火性能有显著影响, 且无论对于开口或闭口压型钢板组合楼板, 楼板厚度越大, 楼板耐火时间越长。楼板厚度每提高10mm, 耐火时间增加10%左右。因此, 可判定楼板厚度是影响组合楼板抗火性能的主要因素之一。
2.5 混凝土强度
取C20, C25, C30, C35, C40五个不同楼板混凝土强度等级进行计算分析。根据挠度达到规范要求限值确定其耐火时间, 并与蒋首超等
由图10可知, 无论闭口型或开口型压型钢板组合楼板, 混凝土强度等级是影响组合楼板抗火性能的主要因素:混凝土强度等级越高, 组合楼板耐火极限越高。同时耐火时间随混凝土抗压强度增加相对均匀, 相关关系较好, 混凝土抗压强度每提高5MPa, 楼板耐火时间提高6%左右。
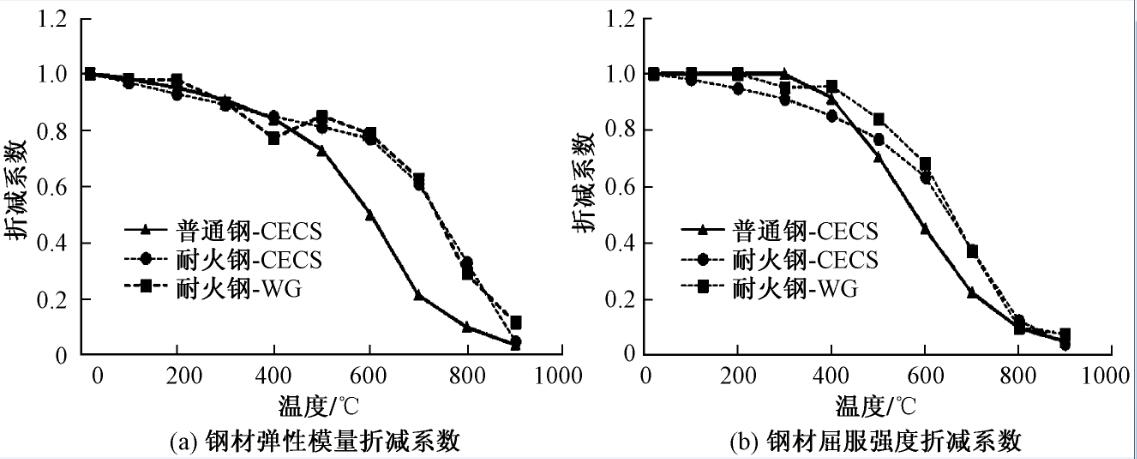
注:普通钢-CECS表示《建筑钢结构防火技术规范》(CECS 200:2006)[7]中普通钢材;耐火钢-CECS表示《建筑钢结构防火技术规范》(CECS 200:2006)[7]中耐火钢;耐火钢-WG表示武钢生产的WGJ牌号耐火钢,余同。
图11 不同温度下钢材材性对比
2.6 钢材耐火性能
为考虑不同钢材耐火性能对组合楼板整体抗火性能和耐火时间的影响, 本文采用钢结构防火规范中普通钢材的屈服强度和刚度折减系数、耐火钢的相关参数以及WGJ牌号耐火钢实测高温折减系数三种本构模型进行参数分析。三种材料的弹性模量以及屈服强度随温度变化的折减系数如图11所示, 图中普通钢-CECS表示钢结构防火规范中普通钢材;耐火钢-CECS表示中耐火钢;耐火钢-WG表示WGJ牌号耐火钢。其中WGJ牌号耐火钢弹性模量和屈服强度的折减系数均由材性试验得到。从材性对比可以看到, 高温下耐火钢的屈服强度和弹性模量下降较少, 屈服强度在600℃时能达到常温时强度的2/3;WGJ牌号耐火钢在屈服强度上表现优于钢结构防火规范规定值, 其高温耐火性更佳。
针对上述三种不同材性的闭口压型钢板组合楼板得到的耐火时间参数分析结果如图12所示。从高温下钢材屈服强度和弹性模量折减系数来看, WGJ牌号耐火钢参数优于钢结构防火规范中的耐火钢取值, 这种耐火性能的优势体现在组合楼板抗火性能中。钢材的耐火性能越好, 组合楼板耐火极限越高, 钢结构防火规范耐火钢可使闭口压型钢板组合楼板的耐火时间在不同荷载水平下提高3.6%~7%;WGJ牌号耐火钢可使闭口压型钢板组合楼板的耐火时间提高6.6%~12%。
2.7 小结
通过各种参数对闭口压型钢板组合楼板抗火性能影响的分析可知, 混凝土及钢材材料强度、楼板及压型钢板厚度、钢材耐火性对组合楼板抗火性能均有不同程度的影响。其中与开口压型钢板组合楼板不同的是, 钢材的相关参数 (厚度、强度等) 仍然会影响组合楼板抗火性能, 为提供承载力发挥作用。这是因为闭口压型钢板组合楼板闭口部分的屏蔽作用, 该部分钢板温度上升慢, 仍可以在升温后期发挥作用。而开口压型钢板组合楼板整块钢板在受火后期温度过高, 难以继续提供承载力。
图13为不同因素对组合楼板挠度发展的影响。图13中圆圈表示楼板挠度发展出现分离点的位置。从图13中可以看出:1) 楼板厚度是影响组合楼板抗火性能最主要的因素, 对受火变形发展全过程都有影响;2) 混凝土强度、钢材强度及厚度对组合楼板变形影响从30~40min开始, 此时钢板底面温度已经达到600℃以上, 高温区逐渐向组合楼板内部蔓延;3) 钢板耐火性对挠度发展影响较晚, 从80min左右开始, 此时钢板闭口部分温度达到600℃, 耐火钢在高温下 (600℃) 强度和刚度折减较小的优势得以发挥。
3 闭口压型钢板组合楼板抗火设计方法
现行钢结构防火规范中针对组合楼板抗火设计的规定源于蒋首超等
式中:RMC为火灾下单位宽度组合楼板素混凝土板的正弯矩承载力;ft为常温下混凝土的抗拉强度设计值;W为单位宽度组合板内低于700℃部分素混凝土板的截面正弯矩抵抗矩;Mmax为火灾下单位宽度组合板内由荷载产生的最大正弯矩设计值;ηF为Mmax与RMC的比值;tr为无防火保护的组合楼板的耐火时间, min。
3.1 温度场简化计算公式
李国强等
式中:T为距组合楼板底面d高度处的截面在受火时间t时的温度;H为楼板厚度。
公式 (2) 考虑了钢板闭口部分对火灾热辐射和热对流的屏蔽作用。115mm厚楼板在30, 60, 90, 120min受火时间下, 组合楼板截面不同高度处的温度公式 (2) 计算值与有限元模拟值对比, 以及公式 (2) 计算和有限元模拟的组合楼板底面和背火面温度随时间变化情况对比如图14所示, 两类曲线有较高的重合度。可见修正后的公式 (2) 适用于闭口压型钢板组合楼板截面温度场分布的计算。
3.2 耐火极限计算方法
参照钢结构防火规范中耐火极限计算方法的计算思路, 考虑闭口压型钢板组合楼板的闭口部分在受火后期升温较低, 且仍能提供部分承载力的特点。将公式 (1a) 中楼板抗力部分修改为常温下由压型钢板闭口部分和素混凝土提供的抗弯承载力, 见图15示意中的红色部分。
根据影响因素的分析, 将不同混凝土强度、楼板厚度、压型钢板相关几何及材料参数考虑在内的耐火时间 (由变形条件得到) 和由公式 (1b) 计算得到的应力比放在图16中。处于安全性考虑, 将回归得到的曲线下移, 使其能包络所有数据点, 可以得到适用于闭口压型钢板组合楼板的计算公式 (3) 。
从图16中可以看到, 闭口压型钢板组合楼板耐火时间数据点以及修正后的公式 (3) 计算的耐火时间均远大于钢结构防火规范中计算的开口压型钢板组合楼板耐火时间。闭口压型钢板组合楼板耐火时间在不同荷载水平下均有大幅度提高。利用公式 (3) 计算本文及文献
耐火时间公式 (3) 计算值与试验结果对比/min 表5
|
实例 |
耐火时间试验值 | 公式 (3b) 计算值 |
|
本文Encondek (150mm) |
172 | 170 |
|
深圳平安[15] |
>90 | 85 |
|
尹晓东等[16] |
118 | 123 |
同时, 根据前述对耐火钢材的参数分析可知, 在不同荷载条件下, 采用耐火钢的组合楼板耐火时间约有10%左右的提高。若采用钢结构防火规范规定的耐火钢, 组合楼板耐火时间可提高8~10min, 若采用WGJ牌号耐火钢, 组合楼板耐火时间可提高15~17min, 且不同荷载水平下耐火时间提高的绝对值相差不大。因此可对公式 (3) 中的截距值进行修正, 得到适用于耐火钢的组合楼板耐火极限计算公式:
式中α为考虑了钢材耐火性的修正系数, 当采用钢结构防火规范规定的耐火钢材时, α取1.04;当采用WGJ版号耐火钢时, α取1.07。
根据试验和有限元分析可知, 厚度较薄的楼板较先达到背火面温升超过140℃的绝热条件, 厚度较厚的楼板较先达到挠度变形限值。利用本文公式 (2) 可以计算得到不同楼板厚度下背火面温升达到140℃的绝热耐火时间, 利用公式 (3) 可以计算得到组合楼板到达变形限值条件下的耐火时间。两种设计条件下的曲线交点如图17所示, 其中图17 (a) 为组合楼板采用C20混凝土, 1mm厚度、屈服强度250MPa闭口压型钢板, 楼面活荷载4kN/m2 (工况1) 时的耐火时间, 图17 (b) 为组合楼板采用C30混凝土, 1mm厚度、屈服强度320MPa闭口压型钢板, 楼面活荷载12kN/m2 (工况2) 时的耐火时间。
采用C20混凝土, 1mm厚度、屈服强度250MPa闭口压型钢板, 楼面活荷载取4kN/m2时, 钢板分别选用普通钢材和耐火钢材, 满足耐火极限90, 120, 180min所需要的楼板厚度如表6所示。
不同耐火极限下楼板厚度表6
|
耐火极限/min |
普通钢材/mm | 耐火钢材/mm |
|
90 |
90.5 | 88.5 |
|
120 |
104.5 | 97 |
|
180 |
125 | 111 |
4 结论
本文对新型闭口压型钢板组合楼板抗火性能影响因素进行了数值参数分析, 并据此提供相关计算方法, 得到如下结论:
(1) 混凝土及钢材材料强度、楼板及压型钢板厚度、钢材耐火性、楼面荷载对组合楼板抗火性能均有不同程度的影响。
(2) 与开口压型钢板组合楼板不同的是, 钢材的相关参数 (厚度、强度等) 仍然会影响闭口压型钢板组合楼板的抗火性能, 为提高承载力发挥作用。这是因为闭口压型钢板组合楼板闭口部分的屏蔽作用, 该部分钢板温度上升慢, 仍可以在升温后期发挥作用。
(3) 本文提出了闭口压型钢板组合楼板温度场简化计算公式以及适用于该类组合楼板的耐火时间计算方法, 考虑了压型钢板闭口部分的作用;同时给出考虑钢材耐火性的修正计算公式, 可用于计算采用耐火钢的组合楼板的耐火时间。
(4) 闭口压型钢板组合楼板耐火极限控制条件下, 楼板临界厚度在130~140mm之间, 低于临界厚度的楼板先达到背火面温升140℃绝热条件;高于楼板临界厚度先达到挠度变形限值条件。
(5) 闭口压型钢板组合楼板相对于开口压型钢板组合楼板而言, 可提高至少50%耐火时间。若采用耐火钢材, 耐火极限可进一步提高5%~15%。
[2] BREKELAMANS JW PM, HAARPW V D, TWILTL, et al. The mechanical behavior of simply supported fire-exposed composite steel/concrete slabs[R]. Netherlands:Eindhoven University of Technology/TNO Delft, 1990.
[3] HAMERLINCK A F. The behaviour of fire-exposed composite steel/concrete slabs[D]. Eindhoven, Netherlands:Eindhoven University of Technology, 1991.
[4] PANTOUSA D, MISTAKIDIS E. Advanced modeling of composite slabs with thin-walled steel sheeting submitted to fire[J]. Fire Technology, 2013, 49 (2) :293-327.
[5] 董建莉, 高立堂, 韩金生. 压型钢板-砼组合楼板火灾下温度场的数值分析[J]. 青岛理工大学学报, 2006, 27 (4) :19-22.
[6] 蒋首超, 李国强, 楼国彪, 等. 钢-混凝土组合楼盖抗火性能的数值分析方法[J]. 建筑结构学报, 2004, 25 (3) :38-44.
[7] 建筑钢结构防火技术规范:CECS 200∶2006[S].北京:中国计划出版社, 2006.
[8] Design of composite steel and concrete structures part 1-2:BS EN 1994-1-2[S]. London:British Standards Institution, 2005
[9] LIE T T, KODUR V K R. Fire resistance of circular steel columns filled with bar-reinforced concrete[J]. Journal of Structural Engineering, 1996, 120 (5) :30-36.
[10] 李卫, 过镇海. 高温下砼的强度和变形性能试验研究[J]. 建筑结构学报, 1993, 14 (1) :8-16.
[11] 王元清, 成钟寿, 石永久. 闭口型压型简支组合楼板承载力有限元分析[J]. 沈阳建筑大学学报 (自然科学版) , 2011, 27 (5) :833-838.
[12] 蒋首超, 李国强, 楼国彪, 等. 钢-混凝土组合楼盖抗火性能的数值分析方法[J]. 建筑结构学报, 2004, 25 (3) :38-44.
[13] 李国强, 韩林海, 楼国彪, 等. 钢结构及钢-混凝土组合结构抗火设计[M]. 北京: 中国建筑工业出版社, 2006.
[14] 李国强, 殷颖智, 蒋首超. 火灾下组合楼板的温度场分析[J]. 工业建筑, 1999, 29 (12) :47-49.
[15] 霍宗诚, 陆建新, 胡攀, 等.深圳平安金融中心组合楼板设计与施工[J].建筑结构, 2015, 45 (1) :5-9.
[16] 尹晓东, 郭彦林, 马智刚, 等. 闭口式压型钢板-混凝土组合楼板耐火试验研究[J]. 建筑结构, 2005, 35 (1) :53-54.















