CFG桩复合地基具有施工速度快、造价低、地基承载力高等优点, 从20世纪80年代推广应用至今, 在高层和超高层建筑中得到了广泛的应用^[1,2]。与此同时, 由于地质勘察不够详细、设计方案因素、施工质量等方面原因造成的高层建筑倾斜问题日益凸显。不同建筑结构形式和地基处理方式适用的纠倾方式不尽相同, 低层和多层建筑纠倾理论不能完全胜任各种复杂工程。纠倾主要依靠技术人员的经验, 主观性较强, 且高层建筑纠倾工程可参考的经验方法匮乏^[3,4]。同时, 由于学科的理论研究落后于工程实践, 各种纠倾方法相关理论的研究还不完善^[5]。

　　 目前浅层掏土法在CFG桩复合地基中的应用尚未见到类似工程实例, 且其纠倾机理与单纯的浅层掏土方法有很大不同, 相关机理与设计方法还缺乏更深入系统的理论研究, 因此, 本文研究成果具有广泛的应用价值与社会意义。

　　 CFG桩复合地基的承载机理与浅基础有明显不同, CFG桩复合地基通过CFG桩体与地基的协同作用共同承担上部结构的荷载。在基底下浅层掏土过程中, 基底下土体面积减小, 一部分上部荷载转移到CFG桩身之上, 如图1 (a) 所示, 其中阴影部分为每根桩所承担的受力面积。同时由于基底下整体受力面积的减小, 地基附加应力相应增大, 从而导致地基再次产生压缩变形。从力学原理上看, CFG桩复合地基中的浅层水平掏土是通过应力解除使土体发生塑性流动, 影响基底土体发生向掏土孔的变形, 从而改变基底的应力面积, 发生附加变形。相比于浅基础下的掏土方法, 此种方式的纠倾难度更大。

　　 鉴于实际地基组成类型以及土应力条件十分复杂, 在研究地基中土孔的掏土问题时, 要做一些假定来近似求解。假定如下: 1) 假设所求解的问题为平面应变问题;2) 所研究的地基土为均质各向同性的材料, 且可压缩变形;3) 与外荷载所产生的应力相比, 体力效应忽略不计, 掏土孔各向应力相等, 由基尔希公式^[6]可知, 掏土孔周边应力分布相同, 形成的塑性区域为圆形。

　　 浅层掏土设计时, 首先计算掏土孔的塑性区域, 要让塑性区域影响到基底范围。假定塑性区域与基底交点的水平距离为dl′, 塑性区影响厚度为dh, 由几何关系:

　　 $\text{d}{l}^{\prime }=2(\text{d}h-R{}_{\text{Ρ}})\times \tan \left[\arccos \left(\frac{\text{d}h-R{}_{\text{Ρ}}}{R{}_{\text{Ρ}}}\right)\right](1)$

　　 式中R_p为塑性区半径。

　　 掏土方向单位长度塑性区在地基中的体积ΔV₁为:

　　 $\begin{array}{c}\text{Δ}V{}_1=\frac{360-2\arccos \left(\frac{\text{d}h-R{}_{\text{Ρ}}}{R{}_{\text{Ρ}}}\right)}{360}\text{π}(R{}_{\text{Ρ}}){}^2+\hfill \\ (\text{d}h-R{}_{\text{Ρ}}){}^2\times \tan \left[\arccos \left(\frac{\text{d}h-R{}_{\text{Ρ}}}{R{}_{\text{Ρ}}}\right)\right]\hfill \end{array}(2)$

　　 将基底范围下塑性区造成的影响等效为一矩形区域, 由几何关系可以得出矩形区域的宽度:

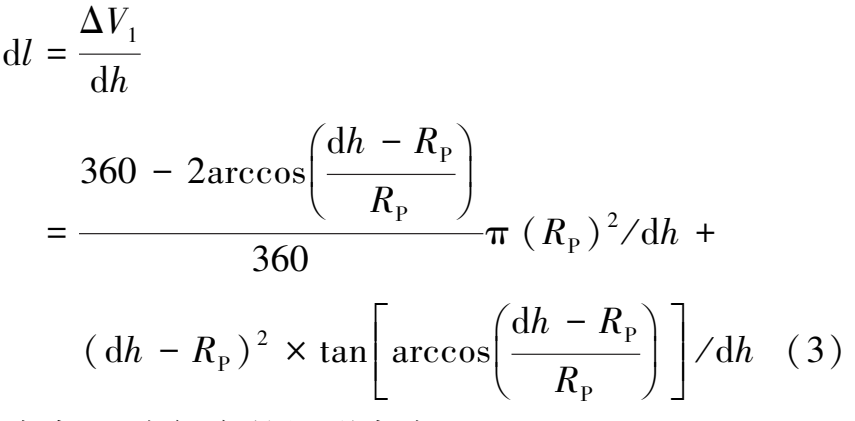
　　 式中dl为假定的矩形宽度。

　　 浅层掏土时, CFG桩复合地基基底下土体被掏出, 影响其范围内的土体向掏土孔位置发生变形, 则等效矩形区域下降的高度dh′为:

　　 $\begin{array}{l}\text{d}{h}^{\prime }=\frac{\text{Δ}V{}_{1^{\prime }}}{\text{d}l}\\ =\text{Δ}V{}_{1^{\prime }}/\left[\frac{360-2\arccos \left(\frac{\text{d}h-R{}_{\text{Ρ}}}{R{}_{\text{Ρ}}}\right)}{360}\text{π}(R{}_{\text{Ρ}}){}^2\right]+\\ \text{Δ}V{}_{1^{\prime }}/\left\{(\text{d}h-R{}_{\text{Ρ}}){}^2\times \tan \left[\arccos \left(\frac{\text{d}h-R{}_{\text{Ρ}}}{R{}_{\text{Ρ}}}\right)\right]\right\}\end{array}(4)$

　　 式中ΔV₁′为浅层掏土单位长度上掏出的土体体积。

　　 则掏土后CFG桩复合地基dh′高度范围内基底受力面积发生变化, 再次发生压缩变形, 其值为:

　　 $\text{Δ}\text{Δ}S=\left(\frac{{\rm P}{}_1}{E{}_{\text{s}\text{p}1}}-\frac{{\rm P}{}_0}{E{}_{\text{s}\text{p}0}}\right)\text{d}{h}^{\prime }(5)$

　　 式中:ΔΔS为掏土沉降;P₀为基底初始应力;P₁为掏土后基底应力;E_sp0为复合地基的初始压缩模量, 由复合地基静载荷试验确定;E_sp1为复合地基掏土后压缩模量。

　　 复合地基把加固区土体和桩体视为一种复合土体, 其压缩性用复合模量来评价。复合模量等于加固土体的压缩模量与桩体的压缩模量按照面积置换率进行叠加的结果^[7,8,9], 计算公式为:

　　 $E{}_{\text{s}\text{p}}=mE{}_{\text{p}}+(1-m)E{}_{\text{s}}(6)$

　　 式中:E_p为桩体的压缩模量;E_s为桩间土的压缩模量;m为面积置换率;E_sp为复合地基的压缩模量。其中面积置换率m为:

　　 $m=d{}^2/d{}_{\text{e}}{}^2(7)$

　　 式中:d为桩体的平均直径;d_e为一根桩处理面积的等效圆直径, 正方形布桩时d_e=1.13s, 矩形布桩时$d{}_{\text{e}}=1.13\sqrt{s{}_{1}s{}_2}$, 其中s, s₁, s₂分别为桩间距、纵向桩间距和横向桩间距。

　　 浅层掏土纠倾时, 受扰动土体向下移动后, 基底受力面积减小, 复合地基每根桩承担的处理面积发生变化, 受荷总面积变为:

　　 $\text{Δ}S{}_1{}^2=\text{π}(1.13s){}^2/4-\text{d}{l}^{\prime }s/4(8)$

　　 由面积置换率计算公式得到掏土后复合地基的面积置换率m₁:

　　 $m{}_1=\text{π}d{}^2/4\text{Δ}S{}_1{}^2(9)$

　　 复合地基掏土后压缩模量:

　　 $E{}_{\text{s}\text{p}1}=m{}_{1}E{}_{\text{p}}+(1-m{}_1)E{}_{\text{s}}(10)$

　　 假设上部荷载作用于基底的初始应力为P₀, 则掏土后基底的应力变为P₁:

　　 ${\rm P}{}_1=\frac{{\rm P}{}_0(1.13s){}^2}{\text{Δ}S{}_1{}^2}(11)$

　　 掏土前后基底的应力变化:

　　 $\text{Δ}{\rm P}=\frac{{\rm P}{}_0(1.13s){}^2}{\text{Δ}S{}_1{}^2}-{\rm P}{}_0(12)$

　　 纠倾时CFG桩复合地基的沉降可以表示为:

　　 $S=S{}_1+S{}_2+S{}_3(13)$

　　 式中:S₁为掏土计算厚度dh′范围内的沉降量即纠倾沉降差;S₂为堆载时dh′以下范围复合地基产生的沉降;S₃为桩端下卧层的附加沉降量。

　　 由式 (6) , (12) 进一步可得纠倾过程中掏土、堆载后建筑的总沉降量:

　　 $\begin{array}{l}S=S{}_1+S{}_2+S{}_3=\\ \left(\frac{{\rm P}{}_1}{E{}_{\text{s}\text{p}1}}-\frac{{\rm P}{}_0}{E{}_{\text{s}\text{p}0}}\right)\text{d}{h}^{\prime }+{\displaystyle \sum _{i=2}^n\frac{\text{Δ}p{}_i}{E{}_{\text{s}\text{p}i}}}{\rm H}{}_i+{\displaystyle \sum _{i=n+1}^m\frac{\text{Δ}p{}_i}{E{}_{\text{s}i}}}{\rm H}{}_i(14)\end{array}$

　　 式中:Δp_i为相应计算土层的附加应力值;H_i为相应计算土层的厚度。

　　 CFG桩复合地基浅层掏土纠倾设计时不单要使建筑物回倾到预期值, 而且在纠倾过程中要保证建筑主体、建筑基础、建筑地基不能发生破坏。因此, 在建筑纠倾方案设计时要充分考虑纠倾方案是否会造成基础内力或变形超出允许范围^[10,11,12]。

　　 高层建筑在纠偏回倾过程中线性回倾十分重要, 如果在纠倾过程中, 不能保证建筑物线性变位, 一旦非线性变位程度较大, 这种因纠倾而引起的次生内力也会相应增大, 若超出结构材料承载能力便会造成结构的损坏, 裂缝继续开展、发育, 对主体结构造成严重损害。

　　 建筑发生倾斜后, 沉降量相对较大一侧基底应力相比也较大, 如果要实现建筑的线性回归, 从理论上来说需要对基底下部应力进行控制。首先依照地基应力等值线确定出掏土区, 并根据各个区域的应力大小或需要调整的沉降量大小对掏土区进行划分, 设计时掏土产生的应力在平面上应呈线性分布使建筑回倾。掏土前后基底应力控制情况如图2所示。

　　 综上所述, 为了使建筑在纠倾过程中能够实现线性变位, 最基本的途径就是实现基底应力变化的线性分布。在纠倾工程中可以通过以下两种途径解决:1) 线性掏土实现基底应力分布线性化。但是由于施工工艺限制, 这种掏土方法实际操作难度很大。2) 通过线性加载实现应力的线性分布。通过在建筑内部分区域、分大小施加堆载, 或者通过建筑主体施加锚索拉力的方法, 使产生的荷载分布规律呈线性。

　　 浅层掏土纠倾法的纠偏过程是一个使基底地基应力附加的过程。地基土体内部应力调整时桩基承担的荷载相应增大, 当端承桩和超长摩擦桩受到的上部荷载较大, 然而土 (岩) 体能够提供的竖向荷载大于桩身材料强度所能承受的荷载时, 桩体便会因强度过大而发生破坏。

　　 CFG单桩承载力R_a可以通过下式进行计算:

　　 $R{}_{\text{a}}=u{}_{\text{p}}{\displaystyle \sum _{i=1}^{n}q}{}_{\text{s}i}l{}_i+q{}_{\text{p}}A{}_{\text{p}}(15)$

　　 式中:u_p为CFG桩周长度, m;n为桩长范围所划分的土层数;q_si, q_p分别为桩周第i层土的侧阻力、桩端端阻力特征值, kPa;l_i为第i层土的厚度, m。

　　 为了防止桩体发生材料强度破坏, 需满足:

　　 $R{}_{\text{a}}\le f{}_{\text{c}\text{u}}A{}_{\text{p}}/3(16)$

　　 式中f_cu为在标准养护条件下, 28d的桩体试块的抗压强度平均值。因此, 在纠倾过程中必须满足一定的条件, 避免桩身材料发生破坏。

　　 建筑纠倾完成后需要对前期设置的保护桩进行封桩, 防止在纠倾过程中对地基承载力造成影响从而发生建筑复倾。加固后地基承载力会大大提高, 因此, 在进行地基承载力验算时可以通过后期的地基承载能力进行控制。

　　 进行掏土与堆载纠倾时基础底面的压应力为:

　　 $\begin{array}{l}p{}_{\text{k}}=\frac{G{}_{\text{k}}+{\rm N}{}_{\text{k}}+F}{A^{\prime }}(17)\\ p{}_{\text{k}\text{m}\text{i}\text{n}}^{\text{k}\text{m}\text{a}\text{x}}=\frac{G{}_{\text{k}}+{\rm N}{}_{\text{k}}+F{}_{\text{k}}}{A^{\prime }}\pm \frac{L{}_{\text{p}}}{W}(18)\end{array}$

　　 式中:L_p为建筑物倾斜后基础底面的偏心距, m;N_k为按照荷载效应进行标准组合时, 由建筑物上部结构传递到基础顶面的竖向力;G_k为按照荷载效应进行标准组合时, 由建筑物上部结构传递到基础顶面的竖向力;F_k为联合应用堆载纠倾法时建筑所施加的堆载荷载标准值;p_k为按照荷载效应进行标准组合时基础底面的平均压应力;p${}_{\text{k}\text{m}\text{i}\text{n}}^{\text{k}\text{m}\text{a}\text{x}}$为按照荷载效应进行标准组合时, 基础底面边缘的最大和最小压应力;A′为纠倾后建筑物基础底面的面积;W为建筑物基础底面的截面抵抗矩。

　　 对复合地基的承载力进行控制, 需要满足:

　　 $\begin{array}{l}p{}_{\text{k}}\le f{}_{\text{s}\text{p}\text{k}}(19)\\ p{}_{\text{k}\text{m}\text{a}\text{x}}\le 1.25f{}_{\text{s}\text{p}\text{k}}(20)\end{array}$

　　 式中f_spk为地基承载力特征值。

　　 某高层住宅楼如图3所示。该住宅楼建筑总高度80.7m, 地下1层, 地上26层, 结构形式为剪力墙结构, 基础形式为钢筋混凝土筏板基础, 筏板下地基处理采用CFG复合地基。主体完工后发现该楼出现不均匀沉降, 西北角最大沉降量为114.6mm, 东南角最大沉降量为19.5mm, 经计算东西向、南北向倾斜均超过《建筑地基基础设计规范》 (GB 50007—2016) 要求不大于4/1 000的允许值。

　　 对研究项目所处的场地岩土工程条件、地基土工程特性、以及周围施工环境等多方面进行研究分析, 排除了软弱土层影响、地基承载力问题。通过对倾斜建筑周围工程状况的调查研究, 发现筏板下CFG复合地基桩顶标高为-5.22m (相当于绝对高程49.030m) , 大楼北侧地库独立基础底标高为48.150m, 西侧独立基础底标高为47.700m, 2号楼北侧地库外墙距地下车库外墙4.7～6.1m, 2号楼西侧地库外墙距地下车库外墙8.1m (图4) 。

　　 地下车库基坑底部低于大楼褥垫层, 经过分析初步确定该楼出现不均匀沉降主要原因为西北侧开挖过程中引起大楼西北侧应力解除, 对大楼复合地基褥垫层产生扰动, 致使西北侧沉降量增大。此外, 还导致地下车库基坑开挖后新建建筑一侧地基土体受到影响, 发生向基坑一侧的移动。

　　 根据后期测量数据, 西北角与东南角沉降差达到95.1mm, 初步估算后期沉降差10mm, 建筑需要纠倾的回倾量应该控制在85.1mm。纠倾采用直径150mm钻机将褥垫层下持力层中土掏出。

　　 根据建筑的平面形状, 掏土孔的长度共分成3种:1) 建筑北侧长度8.2m钻孔, 第1轮设置3个, 第2轮钻孔施工中再次设置3个;2) 建筑中部长度14.55m钻孔, 第1轮设置1个, 第2轮钻孔施工中再次设置2个;3) 建筑南侧长度8.55m钻孔, 第1轮设置3个, 在第2轮钻孔施工中再次设置3个, 掏土布置如图5所示。

　　 为了研究本文提出的浅层掏土方法以及止倾方案的有效性, 建立倾斜建筑的数值分析模型, 对建筑基坑开挖导致建筑倾斜影响进行分析, 同时对纠偏过程及止倾时地基的内力及变形分布规律进行分析, 确保施工方案可行。

　　 PLAXIS中使用率最高的一个高级土体模型为土体硬化模型HS, 硬化包括两种类型, 分别是剪切硬化和压缩硬化。土体硬化模型采用双曲线拟合三轴加载下竖向应变ε₁和偏应力q之间的应力-应变关系:

　　 $-\epsilon {}_1=\frac{1}{E{}_i}\frac{q}{1-q/q{}_{\text{a}}}(q<q{}_{\text{f}})(21)$

　　 式中:q_a为抗剪强度的渐进值;E_i为初始刚度;q_f为抗剪强度极限值。E_i和E₅₀之间的关系如下:

　　 $E{}_i=\frac{2E{}_{50}}{2-R{}_{\text{f}}}(22)$

　　 式中:E₅₀为50%强度处的割线模量。

　　 将小应变属性引入到土体硬化本构模型中就形成了小应变土体硬化模型。该模型可以模拟从小应变到大应变范围内土体的不同响应。

　　 由于计算中需要考虑基坑开挖及开槽等工况对本项目住宅楼的影响, 根据地勘资料、现场取土进行室内试验并结合工程经验, 选取计算参数如表1所示。

　　 由于墙体分布形式复杂, 故整个住宅楼结构采用板单元模拟, 建立的住宅楼结构模型如图6所示。

　　 筏板基础厚1m, 采用实体单元、线弹性模型模拟, 西北侧拓宽筏板部分亦同。将CFG复合地基等效为CFG桩长范围内的均匀实体, 主要考虑刚度等效, 按复合地基模量换算原则确定等效模量。西北侧筏板拓宽部分的加芯高压旋喷桩采用PLAXIS 3D中提供的Embedded桩单元模拟, 桩体模量按刚度等效原则确定。阻沉桩及筏板拓宽部分和建筑堆载模型如图7, 8所示。

　　 地下车库基坑开挖部分, 按照建模范围内涉及到的基坑边界, 采用板单元模拟基坑的围护结构, 一次性开挖完成。最终模型网格如图9所示。提取基坑开挖过程中引起的土体总位移矢量图, 如图10所示。由图中可清晰看到基坑侧壁向坑内变形, 基坑周边地表沉降, 坑底回弹变形等土体变形状况。其中水平位移最大值发生在基坑侧壁部位, 达到0.152m, 如图11所示。

　　 对于浅层掏土过程模拟一次完成。掏土结束后地基土体内部的位移状况如图12～14所示。从图中可以看出, 掏土纠倾对于建筑的影响范围最广。通过纠倾施工, 建筑整体向东南方向回倾, 从图12中掏土引起的土体总位移分布云图可以清晰地反映出掏土完成后, 地基土体的位移分布情况为从建筑的东南向西北方向逐级变化, 这构成了建筑线性回归的重要条件。掏土引起建筑下部土体的整体位移达到0.04m, 位于建筑的东南区域。

　　 在掏土纠倾影响下, 从图13, 14中可以看出, 掏土纠倾后, 建筑下部土体水平两个方向的位移分布情况基本呈对称分布, 这表明在纠倾影响下, 建筑整体刚度较好, 建筑的变形基本呈线性分布, 有利于建筑的回倾控制, 且回倾效果较好。

　　 从以上模拟分析结果可以发现, 随着纠倾的实施, 建筑不均匀沉降得到不断纠正。每一项措施对于建筑的影响都会随着工程的进行由建筑的一侧逐渐向另一侧过渡, 从而避免建筑发生突沉。

　　 提取各项施工措施所引起的建筑整体移动情况, 对结果进行汇总可以得出各个阶段建筑物整体的回倾状况:1) 基坑开挖导致建筑物倾斜程度加剧, 建筑顶部水平向最大水平位移值达到0.102 7m。随着建筑内部堆载措施以及掏土纠倾工作的进行, 建筑变形前后重叠程度越来越高, 这表明建筑顶部X向偏移程度越来越小, 即经过最后阶段的纠倾, 建筑物最终纠偏完成。

　　 根据本文提出的计算方法, 将建筑物各角沉降计算结果与最终数值模拟结果进行对比分析, 如图15所示。

　　 由图15可以看出, 理论计算值与数值模拟结果相差不大, 其中东南角需要纠偏量值最大。通过理论计算值与数值模拟结果的对比分析, 纠偏建筑物四个角计算值与模拟值最大差值10.1mm, 误差为12.4%, 最小差值为2mm。表明提出的计算方法能够解决复合地基浅层掏土纠偏设计问题, 可以为相似工程设计提供理论指导。

　　 本文基于浅层掏土方法的基本理论, 研究了CFG桩复合地基上高层建筑纠倾的相关理论及纠倾效果, 得出以下主要结论:

　　 (1) 基于浅层掏土原理, 应用弹塑性力学理论对CFG桩复合地基的模量及沉降计算理论进行了分析, 对浅层掏土在CFG桩复合地基的设计理论进行确定。

　　 (2) 研究给出了CFG桩复合地基上的浅层掏土纠倾相关设计参数, 包括掏土孔的直径、掏土孔的长度、掏土孔的位置以及掏土孔的间距等具体确定方法, 确定了科学合理的掏土纠倾方案。

　　 (3) 为了保证在纠倾过程中安全平稳地对掏土过程进行数值模拟, 对建筑加固纠倾全过程的位移变化情况以及地基土体中内力分布情况进行模拟研究。研究表明, 在纠倾过程中位移变化剧烈的区域以及变化量的大小可以指导纠倾施工的过程。

　　 (4) 通过理论计算值与数值模拟结果的对比分析, 表明提出的计算方法能够解决复合地基浅层掏土纠偏设计问题, 可以为相似工程设计提供理论指导。