基于蒙特卡罗法的十字型件刚度分析
王湛 袁辉 陈士哲. 基于蒙特卡罗法的十字型件刚度分析[J]. 建筑结构,2019,49(12):73-78.
Wang Zhan Yuan Hui Chen Shizhe. Analysis of cruciform-stub stiffness based on Monte Carlo method[J]. Building Structure,2019,49(12):73-78.
0 引言
实际的钢结构梁柱节点不是完全刚接或者理想铰接, 而是处于二者之间、具有一定初始转动刚度
组件法其中一个关键的组件概念是T型件 (T-stub) , 如图1所示。T型件可以模拟以下基本组件:1) 柱翼缘受弯;2) 端板受弯;3) 翼缘夹板受弯;4) 底板受拉后的弯曲。对于工字形或H型梁柱端板连接节点, EC3提出可以用T型件来等效这类节点的端板受弯以及柱翼缘受弯, 但为了有效提高节点域的刚度和承载力, 工程当中通常在柱与梁翼缘等高的地方设置两块横向加劲肋, 如图2 (a) 所示。而EC3仍旧用T型件来等效该部分连接, 忽略加劲肋对该T型件的约束作用, 显然是不合适的。此时的横向加劲肋、柱腹板和柱翼缘已经构成一个整体来承受拉力与弯矩, 不能再将其等效成T型件, 而应该等效成一个新的组件来进行刚度计算, 如图2 (b) 所示, 类似T型件, 本文称该组件为十字型件 (Cruciform-stub) 。该组件并未包含在EC3中。此前, 部分学者
对于一些常用的端板连接梁柱节点, 螺栓数目通常只有4个, 见图2 (a) 。为考察应用十字型件 (特指4个螺栓的十字型件) 的必要性, 本文进行了十字型件与T型件的对比分析。基于有限元模型设置析因实验, 分析影响十字型件初始刚度的各个因素, 然后对十字型件进行理论分析, 最后根据析因实验的结果, 采用蒙特卡罗法对理论公式进行验证, 并提出应用更为简便、准确度更高的十字型件初始刚度经验公式。
1 十字型件的对比分析
为验证应用十字型件的必要性, 把十字型件与T型件以及带加劲肋的T型件进行对比分析, 考察其差异与相同之处。
1.1 十字型件与T型件的对比
十字型件参数示意图如图3所示。对比图3和图1中十字型件与含两排螺栓的T型件各尺寸参数, 发现除十字型件多了两块加劲肋之外, 其余尺寸参数与T型件完全一致。若这两块加劲肋对该组件的初始抗拉刚度影响不大, 则十字型件与T型件可以认为是同一个组件, 反之则表明两者不能认为是同一个组件。本文采用ANSYS有限元模型来对此进行验证。具体参数如表1所示, 建立对称模型, 单元为Solid185三维六面体实体单元, 本构关系采用多线性各向同性强化模型, 计算结果显示十字型件初始刚度为908 743N/mm, T型件的初始刚度为443 024N/mm, 十字型件初始刚度约为T型件的1.75倍。从图4中T型件与十字型件的von Mises应力云图示意中也可看出, 两者翼缘部分的应力分布已经完全不同, T型件的应力分布可以看做在一定范围内沿一个方向大致不变, 而十字型件则由于腹板与加劲肋的共同作用, 翼缘板沿长度和宽度两个方向都有较大的应力, 二者的受力机制有很大区别, 故单独提出十字型件的概念进行分析是非常必要的。
各组件主要参数 表1
| 构件 | b/mm | lcf/mm | leff/mm | tf/mm | n/mm | K/ (N/mm) |
|
十字型件 |
200 | 50 | 200 | 12 | 70 | 908 743 |
|
T型件 |
200 | 50 | 200 | 12 | 70 | 44 3024 |
1.2 十字型件与带加劲肋的T型件对比
在梁上翼缘处设置加劲肋, 则加劲肋、梁腹板和梁翼缘组成了一个带加劲肋的T型件, 如图5所示。对比带加劲肋的T型件与十字型件, 发现两者之间的差异在于带加劲肋的T型件比十字型件缺了一个角。本文同样采用ANSYS有限元软件对缺角对刚度的影响进行分析。
ANSYS有限元分析各参数设置同表1, 二者的von Mises应力云图示意如图5 (b) 所示。对比图4 (b) 与图5 (b) 可以发现二者应力分布基本一致, 缺角部分对整个翼缘的受力情况影响并不大。最后算得带加劲肋的T型件初始刚度为887 639N/mm, 与十字型件的初始刚度908 743N/mm相差幅度较小, 仅为2.4%, 因此带加劲肋的T型件与十字型件可以视为同一个组件, 本文统一称为十字型件。
十字型件除了可以等效带加劲肋的柱翼缘受弯外, 还可以等效带加劲肋的端板受弯, 以及其他带加劲肋的T型件。综上所述, 十字型件的适用情况较多, 且受力机制与一般T型件差异较大, 因此把十字型件独立出来作为一个新的组件, 重新对十字型件的初始刚度进行分析与探索很有必要。
2 十字型件的析因实验
析因实验被广泛应用于生物学、化学等学科, 以研究试验各个影响因素的“主效应”和“交互效应”。近年来也有学者将析因实验的分析方法引入到结构试验当中
类比影响两个螺栓的T型件初始刚度的3个参数:翼缘宽度leff、螺栓距腹板边缘的距离lcf以及翼缘厚度tf, 类推到4个螺栓的十字型件上, 猜想影响十字型件初始刚度的参数有螺栓孔上下、左右的间距、翼缘长度和宽度以及翼缘厚度5个参数, 与T型件相比多了两个参数, 分别是翼缘长度b和螺栓间距n。十字型件主要是考虑其翼缘的抗弯刚度, 因此腹板高度和腹板宽度等与十字型件翼缘尺寸无关的参数, 可认为对十字型件的初始刚度影响不大。
初步分析影响十字型件初始刚度的参数有5个, 分别是leff, lcf, tf, b和n。对5个参数设置两水平的25析因实验来检验其显著性以及分析各参数之间的交互效应。5个参数分别取2个值, 一共有32种组合方式, 参数取值以及有限元刚度计算结果见表2。
对析因实验结果进行方差分析, 由于有限元软件进行重复试验会得到同样的结果, 因此把三交互及以上的交互效应当作试验误差
析因实验参数及刚度计算结果 表2
|
组合 |
tf/mm | leff/mm | b /mm | n/mm |
K/ (kN/mm) |
|
|
lcf=50mm |
lcf=65mm | |||||
| 1 | 8 | 150 | 200 | 70 | 477 896 | 402 609 |
|
2 |
8 | 150 | 200 | 100 | 325 699 | 258 079 |
|
3 |
8 | 150 | 250 | 70 | 485 362 | 433 445 |
|
4 |
8 | 150 | 250 | 100 | 333 525 | 283 613 |
|
5 |
8 | 200 | 200 | 70 | 504 363 | 416 283 |
|
6 |
8 | 200 | 200 | 100 | 364 632 | 280 788 |
|
7 |
8 | 200 | 250 | 70 | 516 862 | 453 142 |
|
8 |
8 | 200 | 250 | 100 | 378 461 | 311 535 |
|
9 |
12 | 150 | 200 | 70 | 851 705 | 715 673 |
|
10 |
12 | 150 | 200 | 100 | 678 653 | 550 540 |
|
11 |
12 | 150 | 250 | 70 | 864 082 | 736 547 |
|
12 |
12 | 150 | 250 | 100 | 703 098 | 599 528 |
|
13 |
12 | 200 | 200 | 70 | 908 743 | 755 080 |
|
14 |
12 | 200 | 200 | 100 | 782 340 | 618 158 |
|
15 |
12 | 200 | 250 | 70 | 928 379 | 785 675 |
|
16 |
12 | 200 | 250 | 100 | 817 697 | 679 672 |
方差分析 表3
|
方差来源 |
平方和 | 自由度 | F值 | 显著性概率Sig. |
|
lcf |
8.42×1010 | 1.00 | 1 422.5 | 0.00 |
|
tf |
1.03×1012 | 1.00 | 17 458.7 | 0.00 |
|
leff |
2.01×1010 | 1.00 | 339.5 | 0.00 |
|
b |
5.50×109 | 1.00 | 92.9 | 0.00 |
|
n |
1.61×1011 | 1.00 | 2 721.2 | 0.00 |
|
lcf×tf |
9.33×109 | 1.00 | 157.7 | 0.00 |
|
lcf×leff |
8.12×108 | 1.00 | 13.7 | 0.00 |
|
lcf×b |
7.27×108 | 1.00 | 12.3 | 0.00 |
|
tf×leff |
3.83×109 | 1.00 | 64.7 | 0.00 |
|
tf×b |
2.43×108 | 1.00 | 4.1 | 0.06 |
|
leff×b |
1.23×108 | 1.00 | 2.0 | 0.17 |
|
b×n |
1.86×108 | 1.00 | 3.1 | 0.10 |
|
leff×n |
1.24×109 | 1.00 | 20.9 | 0.00 |
|
tf×n |
4.38×107 | 1.00 | 0.7 | 0.40 |
|
lcf×n |
4.22×107 | 1.00 | 0.7 | 0.41 |
查F分布表, 得F0.05, 1, 16=4.49, F0.01, 1, 16=8.53。从表3中F值一列可以看出, 5个主效应均有F>F0.01, 1, 16=8.53, 相应的显著性概率也有Sig.=0.00<0.05, 拒绝H0 假设, 说明猜想的5个因素对刚度的影响高度显著。并且, 大部分二阶交互效应例如tf×leff 也有F>F0.01, 1, 16=8.53, Sig.=0.00<0.05, 因此对于十字型件, 各个因素之间的交互效应也不能忽略。
综上所述, 十字型件各因素交互效应高度显著, 只考虑单一因素变化对整个组件刚度的影响会得到错误的结果。而由于交互因素较多, 完整的考虑各个因素之间的交互效应来对十字型件的刚度进行理论推导也是不现实的。
3 基于蒙特卡罗法的十字型件刚度分析
通过分析可知, 采用控制单因素变量的方法对十字型件初始刚度进行分析会得到错误的结果, 而由于十字型件本身的复杂性, 采用力学模型对其进行理论分析得到的结果也比较复杂, 难以在实际节点刚度计算当中使用。近年来蒙特卡罗法被广泛应用于结构可靠性以及结构优化等各个方面
型钢表中HW型钢截面尺寸从100×100~400×400, 但是工程当中梁柱连接节点并不常用太大或太小的截面尺寸。综合考虑, 本文采用蒙特卡罗模拟时, 限定b的范围是200~400mm, leff的范围是150~400mm, tf的范围是8~14mm, 为了不出现螺栓孔在模型外边的情况, lcf的范围是大于40mm且小于0.35b, 螺栓间距n的范围是大于70mm且小于0.7leff。运用MATLAB在上述范围内随机抽取500组参数, 然后运用ANSYS对这500组十字型件进行刚度计算。
3.1 十字型件理论分析
参照文献
式中:m为螺栓到加劲肋边缘的距离, 加劲肋厚度不大时, 可以近似m=0.5n;α为计算梁受剪变形时的截面系数, 对于矩形截面取α=1.2
十字型件初始刚度由公式 (1) 中得出的板件刚度和螺栓抗拉刚度串联得出, 螺栓抗拉刚度根据文献
经计算, 当
3.2 超定方程的求解过程
本文根据蒙特卡罗抽样计算结果, 对公式 (1) 的β1和β2进行修正。采取解超定方程的方法来求解。具体计算原理如下:已知共有n个线性方程, m个参数值, 则第i个线性方程为
可得到方程AX=Z, 如果n>m, 则系数矩阵A矩阵不是方阵, 需要求解超定方程。求解过程如下:
令
要使f (X) 取极小值, 需满足f (X) 导数为0, 即:
其中j=1, 2, …, m, 所以有:
写成矩阵的表达为ATAX=ATb, 此方程又称法方程。GTG是一个m阶的方阵, 且为对称矩阵, 若满秩, GTG正定, 则存在唯一系数向量X解。
3.3 经验公式的提出
基于蒙特卡罗抽样的500组十字型件刚度计算结果, 对β1和β2用解超定方程的方式进行求解, 其中n=500, m=2。解得β1=0.635 , β2=0.654 , 计算结果如图7 (b) 所示。相比文献
导致公式计算准确度不高的原因在于简化力学模型的固有缺陷, 人为地把十字型件的板件拆分成4个固支梁模型, 然后进行线性叠加, 但是其实各个板件之间存在耦合关系, 且各个参数之间存在交互效应, 不能用简单的线性叠加来描述十字型件的刚度。
为了得到能更加合理的描述十字型件刚度增长趋势的公式, 尝试抛弃固有的力学模型概念, 依据现有的500组数据, 对十字型件的初始刚度进行拟合。公式的形式有很多, 但是根据课题组已经进行的研究
式中E′为广义弹性模量, 为待定参数
对该公式进行对数化后, 有:
可以看到, 取对数值后, 公式 (2) 变成6个参数的线性方程, 同样利用解超定方程组方法求解, 其中n=500, m=6。可以很容易求得lnE′, r1, r2, r3, r4和r5这6个参数。最后得到公式如下:
公式 (4) 与散点之间的相关系数为0.706 7, 结果如图7 (c) 所示, 计算结果较公式 (1) 精确。但是却存在量纲不和谐的问题, 导致使用该公式时单位必须有所限定, 影响其推广。
分析可知, 公式 (2) 等式左边量纲为N/mm, 右边系数E′可以认为是杨氏模量E乘以一个无量纲的系数, 杨氏模量的量纲为N/mm2, 而其余5个参数的量纲是mm, 只要在拟合公式的时候增加一个限定条件:r1+r2+r3+r4+r5=1, 即可使方程左右两边量纲相等。加上该限定条件后, 实际上原有的6个参数变成了5个, 即lnE′, r1, r2, r3和r4, 其中r5=1-r1-r2-r3-r4, 代入到公式 (3) 中, 可得:
如公式 (5) 所示, 只要在刚度对数化后的刚度数据中减去lnn, 再同样利用解超定方程组的方法, 可以容易求得lnE′ 和r1, r2, r3, r4。最后得到公式如下:

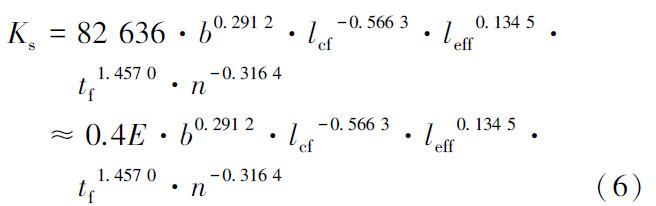
式中E为钢材的杨氏模量, E=2.06×105N/mm2, 为定值。
公式 (6) 与散点之间的相关系数为0.767, 拟合效果与公式 (4) 差距不大, 甚至稍好一些, 如图7 (d) 所示。且方程两边量纲一致, 符合量纲和谐原理。相应的单位可以根据需要进行变化, 计算结果准确度较高, 计算过程较简便。
4 公式的验证
把公式计算结果与析因实验有限元计算结果进行对比, 如表4所示。由于蒙特卡罗抽样范围有所限定, 因此公式的有效应用范围也有一定限制。蒙特卡罗抽样在200mm<b<400mm, 150mm<leff<400mm, 8mm<tf<14mm, 40mm<lcf<70mm, 70mm<n<100mm之间, 公式 (6) 在该区间的计算结果准确度较高。
有限元与公式计算刚度结果对比 表4
|
组合 |
有限元值/ (kN/mm) | 公式计算值/ (kN/mm) | 误差/% |
|
1 |
477 895.55 | 446 288.16 | -6.61 |
|
2 |
325 698.99 | 398 647.36 | 22.40 |
|
3 |
485 361.63 | 476 250.63 | -1.88 |
|
4 |
333 525.49 | 425 411.37 | 27.55 |
|
5 |
504 363.12 | 463 894.93 | -8.02 |
|
6 |
364 631.81 | 414 374.63 | 13.64 |
|
7 |
516 861.97 | 495 039.46 | -4.22 |
|
8 |
378 460.96 | 442 194.51 | 16.84 |
|
9 |
851 705.17 | 805 712.92 | -5.40 |
|
10 |
678 653.07 | 719 703.90 | 6.05 |
|
11 |
864 081.57 | 859 806.10 | -0.49 |
|
12 |
703 098.24 | 768 022.70 | 9.23 |
|
13 |
908 742.75 | 837 499.56 | -7.84 |
|
14 |
782 339.97 | 748 097.35 | -4.38 |
|
15 |
928 379.09 | 893 726.81 | -3.73 |
|
16 |
817 697.49 | 798 322.40 | -2.37 |
|
17 |
402 608.51 | 384 670.82 | -4.46 |
|
18 |
258 078.69 | 343 607.61 | 33.14 |
|
19 |
433 444.99 | 410 496.48 | -5.29 |
|
20 |
283 612.85 | 366 676.41 | 29.29 |
|
21 |
416 282.83 | 399 846.69 | -3.95 |
|
22 |
280 787.89 | 357 163.47 | 27.20 |
|
23 |
453 141.95 | 426 691.21 | -5.84 |
|
24 |
311 535.28 | 381 142.37 | 22.34 |
|
25 |
715 672.56 | 694 471.15 | -2.96 |
|
26 |
550 539.92 | 620 337.07 | 12.68 |
|
27 |
736 547.41 | 741 095.89 | 0.62 |
|
28 |
599 527.71 | 661 984.67 | 10.42 |
|
29 |
755 080.40 | 721 869.13 | -4.40 |
|
30 |
618 158.43 | 644 810.35 | 4.31 |
|
31 |
785 674.69 | 770 333.29 | -1.95 |
|
32 |
679 671.63 | 688 101.01 | 1.24 |
|
平均值 |
5.098 444 | ||
|
标准差 |
12.564 44 | ||
|
变异系数 |
2.464 368 | ||
注:有限元模型参数与表2中参数一致。
当tf=8mm, n=100mm的时候, 此时有限元计算结果比公式计算结果偏小较多, 猜想此类情况产生的原因是500次的蒙特卡罗抽样结果没有涵盖到此情况, 而其余情况下有限元计算值与经验公式计算值差距不大。由于蒙特卡罗法需要循环计算, 需要的时间成本较长, 本文由于时间限制也只抽取了500组十字型件进行计算, 模型样本存在一定缺陷。建立更加简单且有效率的有限元模型, 采用更加合理的抽样机制, 通过本文所采用的方法可以推导出更加准确的经验公式, 并且提升蒙特卡罗法在结构工程当中的应用前景。
5 结论
本文基于带横向加劲肋梁柱节点的组件法, 将带加劲肋的T型件视为一个新组件——十字型件进行分析, 并得出以下结论:
(1) 通过有限元分析, 发现十字型件与T型件的应力分布与传力机制有很大的区别, 单独提出十字型件来进行刚度分析是必要的。
(2) 翼缘宽度leff、螺栓距腹板边缘的距离lcf、翼缘厚度tf、翼缘长度b和螺栓间距n为影响十字型件初始刚度的主要参数, 且部分参数之间存在显著的交互效应。
(3) 基于固支梁模型提出的十字型件理论公式与有限元计算结果有一定的差距, 通过蒙特卡罗法对理论公式进行修正后准确度有一定的提高。
(4) 基于蒙特卡罗法给出了符合量纲和谐原理的经验公式, 该公式应用较为简便, 准确度较高, 有一定的参考意义。
[2] European Committee for Standardizatin.Eurocode 3-design of steel structures part 1.8:design of joints[S].London:British Standards Institute, 2005.
[3] 李国强.半刚性连接钢框架结构设计[M].北京:中国建筑工业出版社, 2009.
[4] MAGGI Y I, GONCALVES R M, LEON R T, et al.Parametric analysis of steel bolted end plate connections using finite element modeling[J].Journal of Constructional Steel Research, 2005, 61 (5) :689-708.
[5] SHI G, CHEN X.Moment-rotation curves of ultra-large capacity end-plate joints based on component method[J].Journal of Constructional Steel Research, 2017, 128 (Complete) :451-461.
[6] 宋佳, 李振宝, 王元清, 等.考虑尺寸效应影响的箍筋约束混凝土应力-应变本构关系模型[J].建筑结构学报, 2015, 36 (8) :99-107.
[7] 张震.实验设计与数据评价[M].广州:华南理工大学出版社, 2014.
[8] 陈志华, 刘占省, 乔文涛, 等.不同拉索种类时弦支筒壳可靠性能及温度影响研究[J].建筑结构, 2010, 40 (7) :112-114.
[9] 李志安, 何江飞, 高博青.大跨度张弦梁结构易损性及评估分析[J].建筑结构, 2013, 43 (2) :41-44.
[10] 潘建荣.基于相关性的框架节点半刚性分析方法研究[D].汕头:汕头大学, 2009.






